티스토리 뷰
반응형
모델 평가 방법
- 좋은 모델을 만들려면 어떤 모델이 좋은 것인가부터 정해야 한다.
평가 메트릭 (Metric)
- Y, N 두 종류 클래스를 분류한다고 해보자.
- 분류 모델에서의 모델 평가 메트릭 (Metric) 은 아래의 두 값의 발생 빈도를 나열한 혼동 행렬으로 부터 계산한다.
- 모델에서 구한 분류의 예측값
- 데이터의 실제 분류인 실제 값
혼동행렬(Confusion Matrix)

- 혼동 행렬의 각 셀에 붙은 이름은 아래 설명과 같다.
- True & False : 예측이 정확했는지를 뜻한다.
- Positive & Negative : 모델을 통해 예측한 값을 의미한다.
- 예를 들어, True Positive (TP) 는 예측이 정확했고 (True), 이때 예측값은 Positive (즉, Y) 였음을 뜻한다.
- 또 다른 예로, False Positive (FP) 는 예측이 틀렸고 (False), 이때 예측값은 Positive (즉, Y) 였음을 뜻하며, 틀렸으니 실제 분류는 Negative (즉, N) 다.
혼동 행렬로부터 계산할 수 있는 계산 메트릭 종류
정확도 (Accuracy)
\(Accuracy \, =\) \(TP \, + \, TN\over TP \, + \, FP \, + \, FN \, + \, TN\)
- 전체 예측에서 (Y, N 상관없이 모두) 옳은 예측의 비율이다.
- 직관적으로 이해하기 쉬워서 많이 사용한다.
- 하지만, 데이터가 불균형 (특정 클래스 비율이 높다면) 하다면, 제대로 평가하기 어렵다.
정밀도 (Precision)
\(Precision \, =\) \(TP\over TP \, + \, FP\)
- Y로 예측된 것 중 실제로도 Y인 경우의 비율이다.
재현율 (Recall)
\(Recall =\) \(TP\over TP+FN\)
- 실제로 Y인 것들 중 예측이 Y로 된 경우의 비율이다.
- TP (True Positive) Rate, Hit Rate, Sensitivity (민감도) 로도 부른다.
- 통계학에서는 Sensitivity로, 다른 분야에서는 Hit Rate 로도 부른다고 한다.
정밀도 (Precision) 와 재현율 (Recall) 의 Trade-Off
- 정밀도와 재현율 모두 실제 정답이 Y인데 모델이 Y라고 예측한 경우에 집중되 있으나, 바라보는 관점이 다르다.
- 정밀도는 모델의 입장에서, 재현율은 실제 정답 (Data) 의 입장에서 정답을 맞춘 경우롤 바라본다.
- ex) 100개의 데이터 중 90개가 Y이고, 10개가 N인데, 확실하게 5개만 Y라고 예측한다면, 당연히 Y라고 예측한 데이터 중 실제 Y (Precision) 인 데이터는 100%가 나온다.
- 하지만, 이러한 모델이 이상적인 것은 아니며, 실제 Y인 90개 데이터 중 Y를 예측한 경우의 수도 고려해야 한다.
- Precision과 Recall을 함께 고려하면, 실제 Y 데이터의 입장에서 우리 모델이 Y라고 예측한 비율을 함께 고려하게 되어 제대로 평가가 가능하다.
- 이 두 지표는 서로 Trade-Off 관계이며, 상호보완적으로 사용할 수 있고, 두 지표값이 모두 높을수록 좋은 모델이다.
- 아래 그래프는 여러 기법들에 대한 정밀도와 재현율의 Trade-Off를 보여주는 하나의 예시이다.
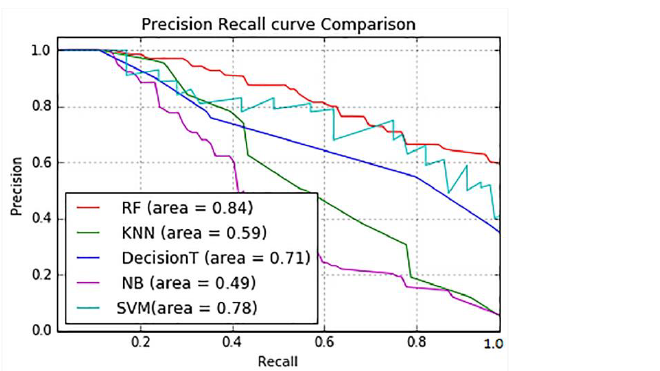
AP (Average Precision)
- Precision-Recall 그래프는 알고리즘의 전반적인 성능을 파악하기 좋지만, 정량적 (Quantitavely) 으로 평가하기에는 불편한 점이 존재한다.
- AP는 Precision-Recall의 알고리즘 성능을 하나의 수치로 평가하기 위해 나온 개념이며, 그래프 선 아래쪽 면적으로 계산된다.
- AP는 보통 컴퓨터 비전에서 Object Detection & Image Classification 알고리즘의 성능을 평가하는 데 사용한다.
특이도 (Specificity)
\(Specificity =\) \(TN\over FP+TN\)
- 실제로 N인 것들 중 예측이 N으로 된 경우의 비율이다.
- True Negative Rate 로도 부른다.
FP-Rate
\(FP-Rate =\) \(FP\over FP+TN\)
- 실제 값이 N인 것들 중 Y로 예측한 비율이다.
- 1 - Specificity 와 같은 값이다.
- False Alarm Rate 로도 부른다.
F1-Score
\(F1\)-\(Score \, = \) \(2 \over Precision^{-1} \, + \, Recall^{-1}\)
\(=\) \(2 \, \times\) \(Precision \, \times \, Recall \over Precision \, + \, Recall\)
- Precision과 Recall의 조화 평균 (Harmonic Mean) 을 이용한 Score이다.
- 조화 평균을 통해 큰 값의 편향 (Bias) 의 영향이 줄어들기 때문에, 데이터가 불균형할 때 평가하는 지표로 사용한다.
- 시스템의 성능을 하나의 수치로 표현하기 위해 사용하는 점수로, 0 ~ 1 사이의 값을 가진다.
- Precision과 Recall 두 값이 균형있게 클 때, 큰 값을 가진다.

ROC (Receiver Operator Characteristic) Curve
- ROC Curve는 점수 기준을 달리할 때, TP Rate와 FP Rate가 어떻게 달라지는지 그래프로 표시한 것이다.
- 바꿔 말하면, FP Rate 대비 TP Rate의 변화를 의미한다.
- y축에 Recall (Sensitivity) 을 표시하면서, x축에는 아래와 같이 두 가지 형태로 표시할 수 있다.
- x축 왼쪽에 1부터 오른쪽에 0까지 표시한다. -> 1 - Specificity = FP-Rate
- x축 왼쪽에 0부터 오른쪽에 1까지 표시한다. -> Specificity
- ROC Curve에서 대각선은 쓸모없는 '랜덤한 분류분석기'를 나타낸다.
- 쓸모없는 예측, 즉 단순히 랜덤하게 성공 / 실패를 예측하는 모형은 어떤 분계점에서도 TPR = FPR이므로 ROC 평면 상에서 대각선에 해당하는 것이다.
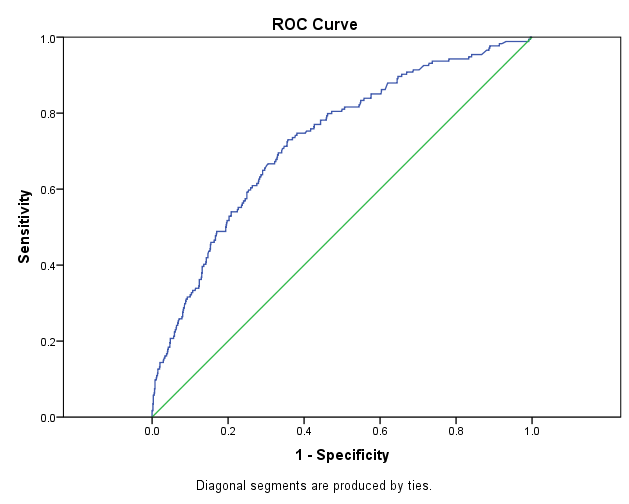
AUC (Area Under the Curve)
- ROC Curve를 그린 뒤, 그 아래의 면적을 지칭하는 말이며, 모델 간 성능 비교에 사용한다.
- 아래 그림에서는 빨간색으로 빗금친 영역을 말한다.
- 위에서 언급한 쓸모없는 랜덤 분류분석기의 AUC는 0.5이며, 좋은 분류분석기일수록 1.0에 가깝다.

Reference
반응형
'ML (Machine Learning)' 카테고리의 다른 글
| [Ridge, Lasso, Elastic Net] Regression (1) | 2019.06.10 |
|---|---|
| 랜덤 포레스트(Random Forest) (0) | 2019.05.15 |
| 편향 (bias) & 분산(Variance) (0) | 2019.04.27 |
| 의사 결정 나무(Decision Tree) (1) | 2019.04.23 |
| Logistic Regression (로지스틱 회귀) (0) | 2019.04.08 |
댓글
