티스토리 뷰
Random Forest란?
Decision Tree를 여러 개 만든 다음 앙상블 (Ensemble) 하여 학습성능을 높이는 방법이다. 이름에서 보이듯이 Tree를 여러 개 만들기 때문에 Forest란 이름이 붙여졌다.
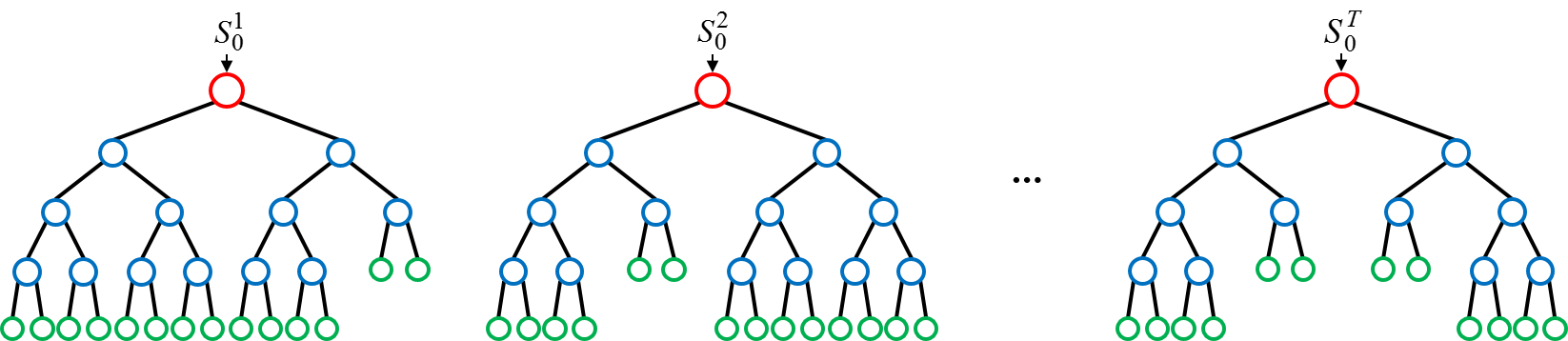
Random Forest 과정
Random Forest 과정은 Decision Tree에서 몇가지 더 추가됐다. Decision Tree를 여러 개 만드는 것이기 때문에 추가된 과정들을 설명한다.
- Bagging을 사용하여 BootStrap을 만든다.
- BootStrap을 이용하여 Decision Tree를 학습시킨 후 예측을 수행한다.
- 1, 2 번을 충분히 반복하여 여러 개의 Decision Tree에 대한 예측을 모은다.
- 회귀트리의 경우 모인 예측들에 평균 (Average) 을 취하고, 분류트리의 경우 다중 투표 (Majority Vote) 를 통해 가장 많은 투표를 받은 범주를 채택하여 최종적인 앙상블 모델의 결과를 도출한다.
Tree는 작은 편향과 큰 분산을 갖기 때문에 매우 깊이 성장한 Tree는 Overfitting이 발생하게 된다.
BootStrap 과정은 Tree들의 편향은 그대로 유지하면서, 분산은 감소시키는 과정으로 따라서 Random Forest의 성능을 향상시킨다. 즉, 한 개의 Decision Tree의 경우 노이즈에 민감하지만, Tree들이 서로 상관화(correlated)되어 있지 않다면 여러 Tree들의 평균은 노이즈에 대해 강인해진다.
Forest를 구성하는 모든 Tree들을 동일한 데이터셋으로만 훈련시키게 되면, Tree들의 상관성은 굉장히 커질 것이다. 따라서 Bagging은 서로 다른 데이터셋들에 대해 훈련 시킴으로써, Tree들을 비상관화시켜 주는 과정이다.

Random Forest의 중요 Parameters
- Decision Tree의 갯수
- Forest가 작으면 Tree들을 구성하고 테스트 하는데 걸리는 시간이 짧은 대신, 일반화 능력이 떨어져 틀린 결과를 낼 확률이 높다.
- 반면에 Forest의 크기가 크다면 훈련 및 테스트 시간은 증가하지만, Forest의 결과값은 각 Tree의 결과들에 평균을 취한 것으로 큰 Forest의 결과값은 작은 Forest보다 일반화 능력이 우수하다.
- Tree의 최대 깊이
- 한 개의 Tree에서 Root 노드부터 Terminal 노드까지 최대 몇 개의 토드를 거칠 것인지를 결정한다.
- 노드 분할 함수 (Split Function)
- 간단하게 요약하면 몇 개의 특징(feature)들만을 선택하는 것이다. 이 과정은 특징 배깅(feature bagging)이라고도 불리며 특징을 선택하는 이유는 배깅을 통해 얻은 트리들 간의 상관성에 있다.
- 즉, 한 개의 특징 또는 극소수의 특징들이 결과에 대해 강한 예측 성능을 지닌다면, 훈련 과정 중 여러 트리 노드에서 이러한 특징들이 중복되어 선택되고 결과적으로 트리들이 상관화되기 때문이다.
- 큰 중요도 점수를 가지는 변수는 작은 값을 갖는 변수보다 높은 순위의 중요성을 갖게된다.
- 이외에도 여러가지가 있으니 맨 아래의 위키피디아 홈페이지를 참고하면 좋을 것 같다.
Random Forest의 성능 평가 : OOB (Out-Of-Bag) error
Random Forest를 구성하는 과정에서 각 데이터 포인트에 대한 OOB error가 구해진다.
먼저 OOB 데이터는 BootStrap을 통한 랜덤으로 중복추출 했을 때 train 데이터에 속하지 않는 데이터를 말하며, OOB error는 BootStrap에 포함되지 않은 데이터를 Decision Tree를 통해 나온 예측값과 실제 값의 차이이다.
즉, Bagging을 통해 만들어진 BootStrap이 train 데이터가 되고 BootStrap에 속하지 않은 데이터가 test 데이터가 되는 것이다. (만약 훈련과정에서 Bagging을 사용하지 않는다면, OOB 데이터 대신 독립된 test 데이터를 이용해 오차를 계산할 수도 있다.)
Reference
'ML (Machine Learning)' 카테고리의 다른 글
| [Ridge, Lasso, Elastic Net] Regression (1) | 2019.06.10 |
|---|---|
| 편향 (bias) & 분산(Variance) (0) | 2019.04.27 |
| 의사 결정 나무(Decision Tree) (1) | 2019.04.23 |
| Logistic Regression (로지스틱 회귀) (0) | 2019.04.08 |
| 분류 성능 모델 평가 지표 (0) | 2019.04.07 |
