티스토리 뷰
Abstract
다음과 같이 독립변수가 p개인 다중 선형 회귀 식이 있다.

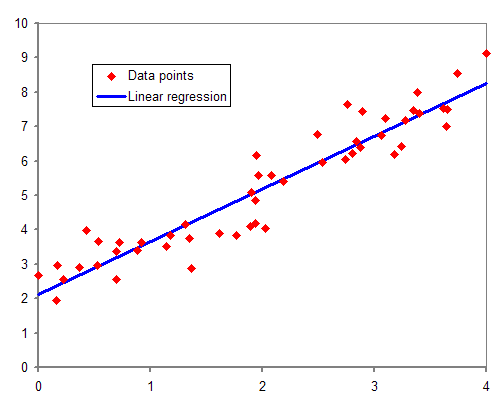
선형 회귀는 종속변수 y가 연속형이며, 아파트 가격을 예측 하는 것이 하나의 예시가 될 수 있을 것이다.
선형 회귀는 독립변수 x와 종속변수 y의 관계가 선형이라고 가정하고, 이를 가장 잘 설명하는 회귀계수들을 데이터로부터 추정하는 모델이다. 선형 회귀의 그래프를 그려보면 아래와 같다.
하지만, 종속변수 y가 범주형 변수라면, 어떻게 될까?

타이타닉 데이터를 예로 들었을 때, 왼쪽그림과 같은 경우 0 = 사망, 1 = 생존 인데 선형 회귀로는 잘 설명하지 못한다.
선형 회귀의 경우 숫자가 의미 있지만 방금과 같은 경우에서 숫자는 의미가 없다. 생존 - 생존 = 사망 이라는 식이 말이 안된다는 이야기다.이러한 사례 때문에 오른쪽 그림과 같은 로지스틱 회귀 모델이 제안되었다. 실제로 변수와 확률 값의 관계가 선형이 아닌 S-커브 형태를 따른다고 한다.
Logistic Regression
로지스틱 회귀의 주요 용어들
- 오즈 (odds) : '실패' (0) 에 대한 '성공' (1) 의 비율
- 로짓 (logit) : (0 ~ 1 이 아니라) ±∞의 범위에서 어떤 클래스에 속할 확률을 결정하는 함수
- 로그 오즈 (log odds) : 변환 모델(선형)의 종속변수, 이 값을 통해 확률을 구한다.
1. 오즈 (odds)
오즈는 사건이 발생할 확률을 사건이 발생하지 않을 확률로 나눈 비율이다, 오즈의 수식은 다음과 같다.

p(y = 1 | x) 확률 값이 다음 그래프와 같이 1에 가까워질수록 odds 값은 엄청나게 상승할 것이며, 0에 가까워질수록 0에 수렴할 것이다.

odds는 2 가지 한계가 있는데,
- 0 < odds < ∞의 범위에 속하기 때문에, 범위에 제약이 있다.
- 위의 그래프와 같이 확률 값과 odds 값은 비대칭성(Asymmetric)을 띈다.
2. 로짓 (Logit), 로그 오즈(Log odds)
이러한 한계를 극복하기 위해서 다음과 같이 로그함수를 취한다.

결국, log(odds)의 범위는 다음과 같이 형성되며,
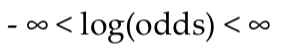
대칭성 또한 가지게 된다. 또한, 성공확률이 0.5를 기준으로 양수와 음수를 가지게 된다.
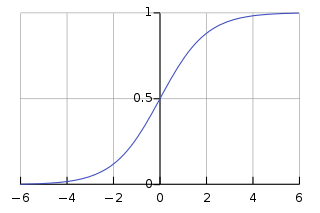
로지스틱 회귀는 이항 또는 다항이 될 수 있다.
- 이항 로지스틱 회귀 : 종속 변수가 (성공, 실패)와 같은 binary 형태
- 다항 로지스틱 회귀 : 종속 변수가 (삼성, LG, 애플)과 같이 3개 이상의 Multi 형태
그리고 예측변수에 로지스틱 반응 혹은 역 로짓 함수를 적용해서 모델링한다.
- 로그 오즈를 이용한 회귀분석 식은 다음과 같으며,

- 양변에 로그를 제하면,
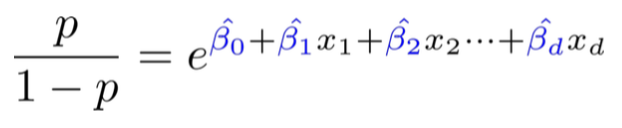
- 마지막으로 성공확률에 대한 식으로 표현하면,

요약해보자면, 로지스틱 회귀에서

이 식의 좌변은 0 or 1 아니면 0, 1, 2, 3 ... 등의 범주값이고, 우변은 ±∞의 범위의 값이 나온다. 그렇게 되면 좌변과 우변의 값이 맞지 않는다. 따라서, 값들을 맞춰주기 위해서 좌변인 y값을 Logit 변환을 해준다.
Logit 변환이란, Odds에 log를 씌운 것인데, 일반회귀식으로는 0 또는 1을 예측할 수 없으므로 y값을 Odds 비로 변환하여 예측한다.
3. 최대 우도 추정법 (MLE:Maximum Likelihood Estimation)
최대 우도 추정법은 확률 모형의 모수 추정에서 일반적으로 사용하는 방법이다.
데이터가 임의의 파라미터 θ에 의존하는 확률분포를 따르고 표본데이터 (아래) 가 주어졌을 때,

데이터가 발생할 확률 (아래) 를 구하고 싶다.

하지만 현재 우리는 θ를 모르기 때문에, 베이즈 규칙을 이용하여 θ가 발생할 우도 (Likelihood, 이미 주어진 표본 x들에 비추어 봤을 때 모집단의 모수 θ에 대한 추정값)로 바꿔서 생각할 수 있다.

위의 경우 가장 적절한 θ는 우도를 가장 최대화 해주는 값이 될 것이다. 즉, 관측된 데이터가 발생할 경우를 가장 높게 만들어주는 값이다.
베르누이 실행 (Bernoulli Trial)
베르누이 실행이란 두 가지 결과만을 가지는 실험을 가리킨다. 베르누이 실행의 결과에 따라 0 (실패) 또는 1 (성공)의 값을 대응시키는 확률 변수 (Random Variable) 를 베르누이 확률변수 라고 한다. 이 확률변수의 확률분포를 베르누이 확률분포 라고 한다.
베르누이 확률변수 Y의 분포는 다음과 같다.
| Y | 0 | 1 |
| P(Y = yi) | 1 - p | p |
위 표를 수식으로 정리하면 아래와 같다.

베르누이 확률변수 Y에 관한 우도함수 (Likelihood Function) 은 다음과 같다.
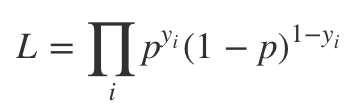
로지스틱 회귀의 우도 함수
i개의 학습 데이터가 있고 정답범주가 2개 (0, 1) 인 이항 로지스틱 모델의 파라미터 β가 주어졌을 때, i번째 관측치의 종속변수 yi에 대해서
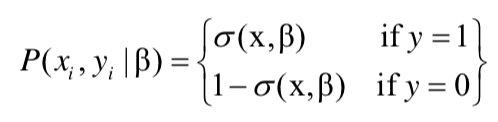
위에서 xi는 i번째 관측치, σ는 로지스틱 함수이며 로지스틱 회귀 우도함수는 다음과 같이 나타낼 수 있다.
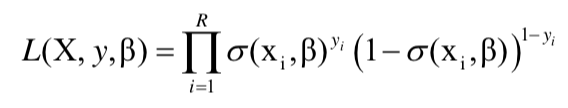
로지스틱 회귀의 파라미터 β는 MLE로 구한다. 로그 우도함수(log-likelihood function)를 최대로 하는 회귀계수 β는 동시에 우도를 최대화하는 β이며 그 역도 성립한다. 식은 아래와 같다.
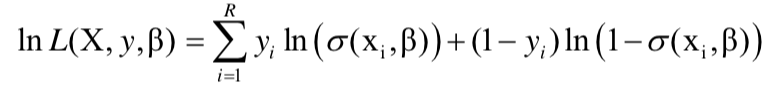
우도함수와 로그 우도함수는 회귀계수 β에 대해 비선형이므로 선형회귀분석과 같이 명시적인 해가 존재하지 않기 때문에 최적화 알고리즘을 통해 해를 구한다. 하나의 예시로 Gradient Descent 알고리즘이 있다.

- 파란색 선 : 가중치 w의 변화에 따른 목적함수 값의 변화
- 검은색 원 : 현재 해의 위치
- 화살표 : 목적함수를 최적화 하기 위해 가중치 w가 이동해야 하는 방향
분류 결과 및 해석
회귀계수가 추정되고 나면 주어진 설명변수집합에 대한 성공확률을 다음과 같이 계산할 수 있다.
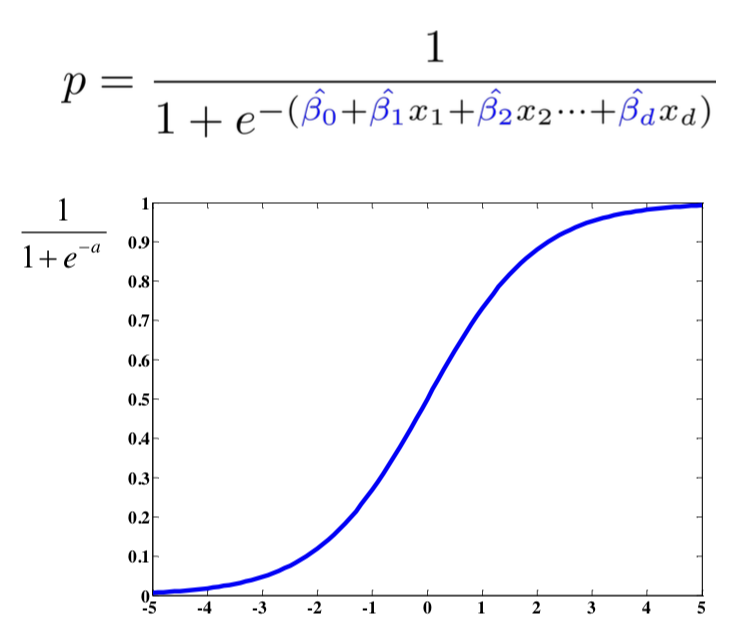
그리고 Binary Classification을 위한 cut-off를 설정한다.

사전확률을 고려한 cut-off나 검증데이터의 정확도를 최대화하는 cut-off 등이 사용될 수도 있다.

로지스틱 회귀분석에서의 회귀계수는 해당 변수가 1 증가함에 따른 로그 승산(odds)의 변화량을 의미한다.
Odds Ratio
로지스틱 회귀분석에서 나머지 변수는 모두 고정시킨 상태에서 한 변수를 1만큼 증가시켰을 때 변화하는 Odds의 비율이다.
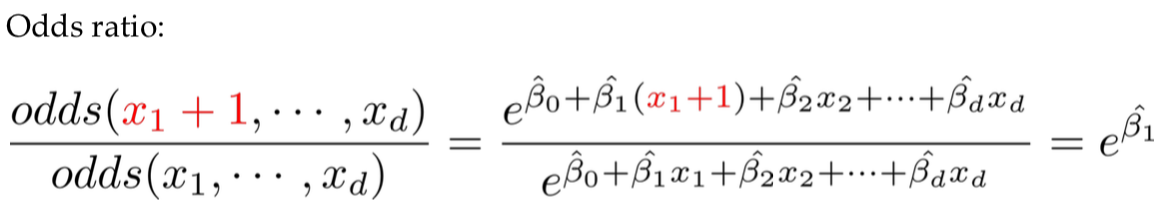
x1이 1만큼 증가한다면 성공에 대한 odds ratio가
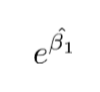
만큼 변화한다.
- 회귀 계수가 양수 -> 변수가 증가하면 성공 확률이 증가 (성공범주와 양의 상관관계)
- 회귀 계수가 음수 -> 변수가 증가하면 성공 확률이 감소 (성공범주와 음의 상관관계)
References
- https://ratsgo.github.io/machine%20learning/2017/04/02/logistic/
- https://nittaku.tistory.com/478
- https://ko.wikipedia.org/wiki/%EB%A1%9C%EC%A7%80%EC%8A%A4%ED%8B%B1_%ED%9A%8C%EA%B7%80
- https://datascienceschool.net/view-notebook/79140e6a9e364bcbb04cb8e525b9dba4/
- https://ratsgo.github.io/machine%20learning/2017/07/02/logistic/
'ML (Machine Learning)' 카테고리의 다른 글
| [Ridge, Lasso, Elastic Net] Regression (1) | 2019.06.10 |
|---|---|
| 랜덤 포레스트(Random Forest) (0) | 2019.05.15 |
| 편향 (bias) & 분산(Variance) (0) | 2019.04.27 |
| 의사 결정 나무(Decision Tree) (1) | 2019.04.23 |
| 분류 성능 모델 평가 지표 (0) | 2019.04.07 |
