티스토리 뷰
반응형
소개
- 주어진 배열을 절반으로 나눠 비슷한 크기를 가진 두 개의 배열을 만든 뒤 정렬한다.
- 평균적으로 \(O(NlogN)\) 의 준수한 성능을 낸다.
- 정렬한 배열을 담을 추가적인 메모리가 필요하다.
과정

코드
public static void Merge(int[] nums, int left, int mid, int right) {
int l = left, r = mid + 1;
int idx = left;
int[] sorted = new int[nums.length];
for (int i = left; i <= right; ++i) {
sorted[i] = nums[i];
}
while (l <= mid && r <= right) {
if (nums[l] < nums[r]) {
nums[idx++] = sorted[l++];
}
else {
nums[idx++] = sorted[r++];
}
}
while (l <= mid) {
nums[idx++] = sorted[l++];
}
while (r <= right) {
nums[idx++] = sorted[r++];
}
}
public static void MergeSort(int[] nums, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
MergeSort(nums, left, mid);
MergeSort(nums, mid + 1, right);
Merge(nums, left, mid, right);
}
}
public static void main(String[] args) {
int[] nums = { 38, 27, 43, 9, 3, 82, 10 };
int len = nums.length;
MergeSort(nums, 0, len - 1);
}
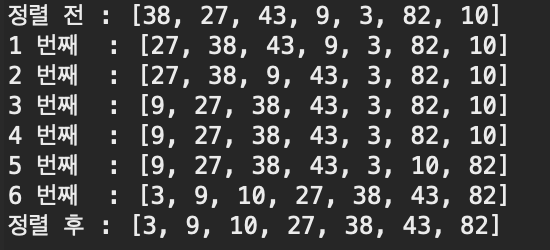
결과
계산 복잡도
Time Complexity
- 배열을 절반으로 쪼개는 과정 : \(O(1)\)
- 모든 배열을 분할하는 과정 : \(O(logN)\) - 첫 번째 분할은 \(N/2, N/2\), 두번째 분할은 \(N/4, N/4, N/4, N/4\)와 같이 진행되어 \(logN\)번 수행
- 나눠져 정렬된 배열들을 다시 병합하는 과정 : \(O(N)\)
- Best : \(O(NlogN)\)
- Average : \(O(NlogN)\)
- Worst : \(O(NlogN)\)
Space Complexity : \(O(N)\) (부분 정렬한 값들을 담을 입력 배열과 동일한 크기의 배열이 필요)
반응형
'Algorithm > Sort' 카테고리의 다른 글
| 퀵 정렬 (Quick Sort) (0) | 2020.12.24 |
|---|---|
| 힙 정렬 (Heap Sort) (2) | 2020.12.24 |
| 셸 정렬 (Shell Sort) (0) | 2020.12.24 |
| 삽입 정렬 (Insertion Sort) (0) | 2020.12.24 |
| 선택 정렬 (Selection Sort) (0) | 2020.12.24 |
댓글
