티스토리 뷰
반응형
소개
- 삽입 정렬의 '배열이 어느정도 정렬되어 있을 때 속도가 빠르다'는 장점을 이용한다.
- 삽입 정렬의 문제점은 요소값들을 삽입할 때 이웃한 위치로 한 칸씩 이동한다는 것이다. 만약 삽입할 요소위치가 현재 위치보다 먼곳에 있다면 불필요한 반복과 비교가 수행된다는 것이다.
- 이러한 점을 보완하여 셀 정렬은 배열을 한 번에 정렬하지 않는다.
- 일정한 기준에 따라 먼저 정렬해야 할 배열을 여러 개의 부분 배열로 만들고, 각 부분 배열을 삽입 정렬을 이용하여 정렬한다.
- 간격 (gap) 이라는 값 (길이 / 2 or 길이 / 3 + 1 ) 을 통해 부분 배열을 만든다.
- 길이 / 2
- 길이 / 3 + 1
- gap이 짝수일 경우 +1 하여 홀수로 만드는 것이 좋다고 한다. (나누는 간격에 의해 성능이 좌우)
과정
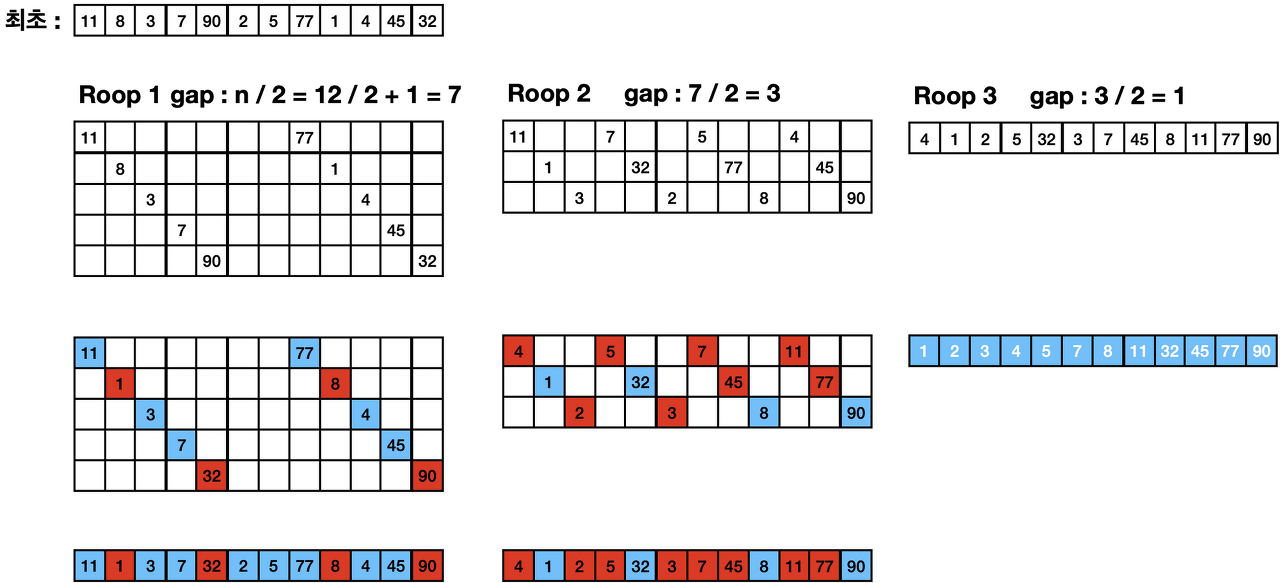
코드
public static void Insertion_Sort(int[] nums, int start, int end, int gap) {
int j;
for (int i = start + gap; i <= end; i += gap) {
int key = nums[i];
for (j = i - gap; j >= start && nums[j] > key; j -= gap)
nums[j + gap] = nums[j];
nums[j + gap] = key;
}
}
public static void Shell_Sort(int[] nums, int len) {
for (int gap = len / 2; gap > 0; gap /= 2) {
if ((gap & 1) == 0)
++gap;
for (int i = 0; i < gap; ++i)
Insertion_Sort(nums, i, len - 1, gap);
}
}
public static void main(String[] args) {
int[] nums = { 11, 8, 3, 7, 90, 2, 5, 77, 1, 4, 45, 32 };
int len = nums.length;
Shell_Sort(nums, len);
}
결과
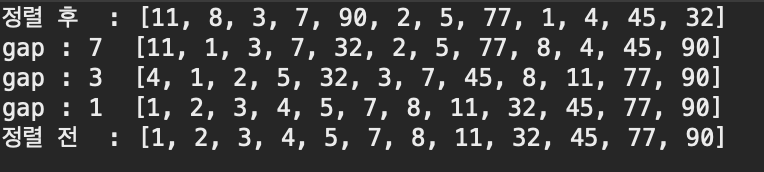
계산 복잡도
Time Complexity
- Best : \(O(N)\) - 삽입 정렬과 마찬가지로 이미 정렬된 경우, 각 값들마다 한 번씩만 확인한다. \((1 + 1 + ... + 1 = N)\)
- Average : \(O(N^{1.3})\) ~ \(O(N^{1.5})\) - 계산하는 방법이 힘들다고 하므로 이렇다라는 것만 알면 될 듯.
- Worst : \(O(N^2)\)
Space Complexity : \(O(1)\)
반응형
'Algorithm > Sort' 카테고리의 다른 글
| 힙 정렬 (Heap Sort) (2) | 2020.12.24 |
|---|---|
| 병합 정렬 (Merge Sort) (0) | 2020.12.24 |
| 삽입 정렬 (Insertion Sort) (0) | 2020.12.24 |
| 선택 정렬 (Selection Sort) (0) | 2020.12.24 |
| 버블 정렬 (Bubble Sort) (0) | 2020.12.24 |
댓글
