티스토리 뷰
반응형
소개
- 현재 인덱스 위치 값과 이미 정렬된 부분 배열의 값들과 비교하여 들어갈 위치를 찾아 정렬한다.
- 성능이 좋아 다른 알고리즘의 일부로도 사용한다.
- 해당 삽입 지점 이후 배열 값들이 한 칸씩 밀리기 때문에 배열 길이가 길수록 효율이 떨어진다.
과정
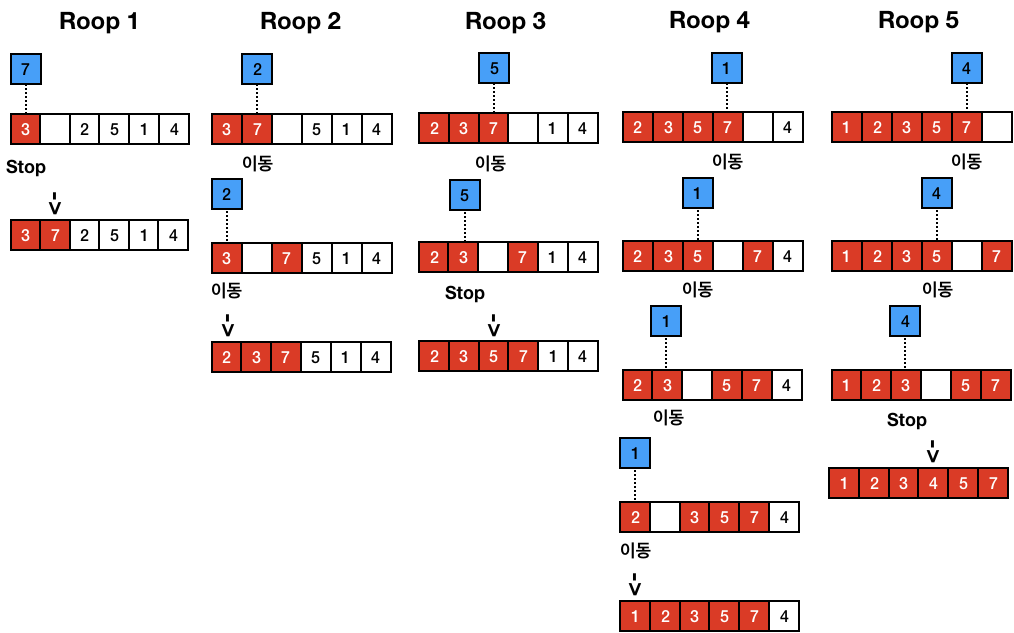
코드
- 첫 번째 인덱스 \(nums[i = 0]\) 의 값은 정렬되어 있다고 가정하고 시작한다.
- compidx를 이용하여 \(i\) 인덱스의 값이 들어갈 인덱스를 정렬된 부분 배열 구간 (\(0\) ~ \(i - 1\)) 에서 찾는다.
public static void main(String[] args) {
int[] nums = { 3, 7, 2, 5, 1, 4 };
int len = nums.length;
for (int i = 1; i < len; ++i) {
int value = nums[i];
int idx = i - 1;
while (idx >= 0 && nums[idx] > value) {
nums[idx + 1] = nums[idx];
--idx;
}
nums[idx + 1] = value;
}
}
결과

계산 복잡도
Time Complexity : \((N-1) + (N -2 ) + ... + 1 = \frac{(N-1)*(N)}{2}\)
- Best : \(O(N)\) - 이미 정렬된 경우, 각 값들마다 한 번씩만 확인한다. \((1 + 1 + ... + 1 = N)\)
- Average : \(O(N^2)\)
- Worst : \(O(N^2)\)
Space Complexity : \(O(1)\)
반응형
'Algorithm > Sort' 카테고리의 다른 글
| 힙 정렬 (Heap Sort) (2) | 2020.12.24 |
|---|---|
| 병합 정렬 (Merge Sort) (0) | 2020.12.24 |
| 셸 정렬 (Shell Sort) (0) | 2020.12.24 |
| 선택 정렬 (Selection Sort) (0) | 2020.12.24 |
| 버블 정렬 (Bubble Sort) (0) | 2020.12.24 |
댓글
