티스토리 뷰
반응형
소개
- 한쪽의 배열에 포함된 값이 다른 쪽 배열의 값보다 항상 작도록 배열을 분할한다.
- 이를 수행하기 위해 파티션 (Partition) 이란 단계를 수행한다.
- 파티션 (Partition) ? - 배열에 있는 수 중 임의의 '기준 수 (Pivot)' 를 지정한 후, 이 기준 수 보다 작거나 같은 숫자를 왼쪽, 더 큰 숫자를 오른쪽으로 보내는 과정이다.
- Pivot에 따라 시간복잡도가 크게 달라진다.
과정

코드
public static int Partition(int[] nums, int left, int right) {
int mid = left + (right - left) / 2;
Swap(nums, left, mid);
int l = left + 1, r = right;
int pivot = nums[left];
while (l <= r) {
while (l < nums.length - 1 && nums[l] < pivot) {
++l;
}
while (r > 0 && nums[r] > pivot) {
--r;
}
if (l <= r) {
swap(nums, l++, r--);
}
}
nums[left] = nums[r];
nums[r] = pivot
return r;
}
public static void QuickSort(int[] nums, int left, int right) {
if (left < right) {
int pivot = Partition(nums, left, right);
QuickSort(nums, left, pivot - 1);
QuickSort(nums, pivot + 1, right);
}
}
public static void main(String[] args) {
int[] nums = { 38, 27, 43, 9, 3, 82, 10 };
int len = nums.length;
QuickSort(nums, 0, len - 1);
}
public static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
결과
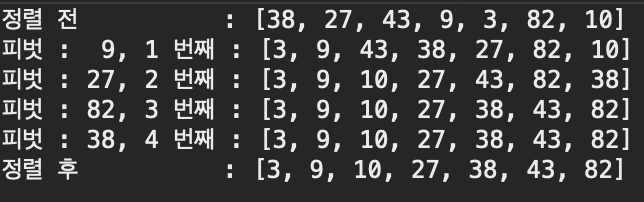
계산 복잡도
Time Complexity
- Pivot과 각 요소 값들을 비교하여 작은 요소를 왼쪽, 큰 요소를 오른쪽으로 정렬하는 과정 : \(O(N)\)
- 배열 길이가 \(2^k\) 라고 했을 때, 절반씩 분할하는 과정 : \(2^{k} -> 2^{k-1} -> ... -> 2^{1} -> 2^{0}\) 으로 \(k = log_{2}N\)
- Best : \(O(NlogN)\)
- Average : \(O(NlogN)\)
- Worst : \(O(N^2)\) - 이미 정렬된 배열의 경우, 분할하는 과정이 깊이 \(N\) 까지 가기 때문에 \(O(N * N) = O(N^2)\)
Space Complexity : \(O(1)\)
반응형
'Algorithm > Sort' 카테고리의 다른 글
| 정렬 기법 비교 (0) | 2021.10.02 |
|---|---|
| 계수 정렬 (Counting Sort) (0) | 2020.12.24 |
| 힙 정렬 (Heap Sort) (2) | 2020.12.24 |
| 병합 정렬 (Merge Sort) (0) | 2020.12.24 |
| 셸 정렬 (Shell Sort) (0) | 2020.12.24 |
댓글
