티스토리 뷰
Paper/ML (Machine Learning)
LightGBM: A Highly Efficient Gradient Boosting Decision Tree
기내식은수박바 2019. 7. 7. 13:45반응형
논문
Abstract
- GBDT (Gradient Boosting Decision Tree) 는 유명한 머신 러닝 알고리즘이며, XGBoost와 pGBRT 같은 효과적인 구현들이 있음.
- 비록 많은 Engineering 최적화들이 이 구현들에 적용되었지만, 효율성과 Scalability는 Feature 차원이 높고 데이터 크기가 클 경우, 여전히 만족스럽지 못함.
- 핵심 이유는 각 Feature가, 가능한 모든 분할 지점의 Information Gain을 추정하기 위해 모든 데이터 인스턴스를 탐색해야된다는 것이며, 이 작업은 많은 시간을 소비함.
- 이러한 문제를 해결하기 위해, 두 가지 새로운 기법들을 제시함 :
- GOSS \((Gradient\)-\(based\) \(One\)-\(Side\) \(Sampling)\)
- EFB \((Exclusive \, Feature \, Bundling)\)
GOSS (Gradient-based One-Side Sampling)
- 작은 Gradients를 가진 데이터 인스턴스의 상당 부분을 제외하고, 나머지 부분만을 이용하여 Information Gain을 추정함.
- 더 큰 Gradients를 가진 데이터 인스턴스가 Information gain 계산에서 더 중요한 역할을 한다고 증명했기 때문에, GOSS가 훨씬 더 작은 데이터 크기를 가지고 꽤 정확한 Information Gain 추정치를 얻을 수 있음.
EFB (Exclusive Feature Bundling)
- Features 갯수를 감소시키기 위해 상호 배타적 (Mutually Exclusive) Features (즉, 이들은 0이 아닌 값을 동시에 가지는 경우가 거의 없음) 를 묶음 (Bundle).
- 배타적인 Features의 최적 Bundling을 찾는 것이 NP-hard 라는 사실을 증명했지만, 탐욕 알고리즘이 꽤 좋은 근사 비율을 달성할 수 있음 (따라서, 분할 지점 결정의 정확도를 크게 손상시키지 않고 효과적으로 Features 수를 감소시킬 수 있음).
LightGBM
- GOSS & EFB를 사용하여 새롭게 GBDT를 구현한 것을 LightGBM이라 부르겠음.
- LightGBM이 전통적인 GBDT와 거의 동일한 정확도를 얻으면서 동시에, 훈련 과정이 20배 이상 더 빠르다는 것을 보여줌.
1. Introduction
- GBDT는 다음과 같은 특징들 덕에 널리 사용된 머신 러닝 알고리즘임.
- 효율성 (Efficiency)
- 정확도 (Accuracy)
- 해석 가능성 (Interpretability)
- 최근 몇 년 사이, 빅데이터가 등장하면서 (Features & 인스턴스 수 측면에서), GBDT는 새로운 과제들, 특히 정확도와 효율성 사이의 Trade-off 에 직면하고 있음.
- 전통적인 GBDT는 가능한 모든 분할 지점들의 Information Gain을 추정하기 위해 모든 Feature 마다 모든 데이터 인스턴스를 조사해야함.
- 따라서, 계산 복잡도는 Feature & 인스턴스 수에 비례하게 됨.
- 이는 빅 데이터를 다룰 때, 시간을 굉장히 많이 소비하게 만듬.
- 이 과제를 해결하기 위해, Feature & 인스턴스 수를 줄이는 간단한 아이디어가 있음.
- 그러나, 이는 매우 중요한 것으로 판명났음.
- 예를 들어, GBDT에서 데이터 Sampling을 수행하는 방법은 분명하지 않음.
- 부스팅 훈련 과정을 가속화 하기 위해, 가중치에 따라 데이터를 Sampling하는 일부 연구들이 있지만, Sample 가중치가 전혀 없기 때문에 연구들을 GBDT에 직접 적용할 수 없음.
- 이 논문에서는 목표를 위해 두 가지 새로운 기술을 제시함.
GOSS \((Gradient\)-\(based\) \(One\)-\(Side\) \(Sampling)\)
- GBDT의 데이터 인스턴스에 대한 Native 가중치가 없지만, 우리는 서로 다른 Gradients를 가진 데이터 인스턴스가 Information Gain 계산에서 서로 다른 역할을 수행한다고 얘기함.
- 특히, Information Gain의 정의에 따라, 더 큰 Gradients를 가진 인스턴스들 (즉, 덜 훈련된 (Under-trained) 인스턴스) 이 Information Gain에 더 많은 기여를 할 것이라고 봄.
- 따라서, Information Gain 추정 정확도를 유지하기 위해 데이터 인스턴스를 Down Sampling할 때, Gradients가 큰 (즉, Top Percentiles 중 또는 Pre-defined Threshold 보다 더 큰) 인스턴스들을 유지하고, Gradients가 작은 인스턴스들을 무작위로 Drop하는 게 더 나음.
- 우리는 그러한 처리가 특히 Information Gain 값의 범위가 클 경우, 동일한 타겟 Sampling 비율을 이용할 때, 균등하게 무작위로 Sampling하는 것보다 더 정확한 Gain 추정치를 유도할 수 있다는 것을 증명함.
EFB \((Exclusive \, Feature \, Bundling)\)
- 보통 실제 어플리케이션에서, Feature 수가 많지만, Feature 공간은 상당히 Sparse하여 효과적인 Features 수를 감소시키기 위해 거의 손실 없는 접근법을 설계할 수 있는 가능성을 제공함.
- 구체적으로, Sparse한 Feature 공간에서, 많은 Features는 (거의) 배타적임 (즉, 0이 아닌 값을 동시에 가지는 경우가 거의 없음).
- 예시들은 One-hot Features를 포함함 (ex. 텍스트 마이닝에서 One-hot 단어 표현).
- 우리는 그러한 배타적인 Features를 안전하게 Bundle할 수 있음.
- 이를 위해, 최적 Bundling 문제를 그래프 Coloring 문제로 감소시키고 (Features가 상호 배타적이지 않다면 모든 두 개의 Features에 Edges를 추가하고 Features를 Vertics로 취함), 이렇게 바뀐 그래프 Coloring 문제를 일정한 근사 비율을 가진 탐욕 알고리즘으로 해결하여 효율적인 알고리즘을 설계함.
2. Preliminaries
2-1. GBDT and Its Complexity Analysis
- GBDT는 순서대로 훈련된 DT (Decision Tree) 의 앙상블 모델임.
- 각 반복에서, GBDT는 Negative Gradients (잔차 에러 (Residual Errors) 로도 알려져 있는) 를 Fitting하여 DT를 학습함.
GBDT의 주요 비용은 DT를 학습하는 데 있으며, 여기서 시간 소모가 가장 많은 부분은 가장 좋은 분할 지점을 찾는 것임.
- 분할 지점을 찾는 가장 유명한 알고리즘 중 하나는 Pre-sorted 알고리즘이며, 이는 Pre-sorted된 Feature 값에서 가능한 모든 분할 지점들을 열거하는 방법임.
- 이 알고리즘은 단순하며 최적 분할 지점을 찾을 수 있지만, 훈련 속도와 메모리 소모 부분에서는 비효율적임.
- 또 다른 유명한 알고리즘은 Algorithm 1에 보이는 히스토그램-기반 알고리즘임.

- 이 방법은 정렬된 Feature 값에서 분할 지점을 찾는 대신, 연속적인 (Continuous) Feature 값들을 이산적인 (Discrete) Bins에 집어넣고, 이 Bins를 사용하여 훈련 동안 Feature 히스토그램을 구축함.
- 히스토그램 구축에 대해 \(O(\#data \, \times \, \#feature)\), 분할 지점 탐색에 \(O(\#bin \, \times \, \#feature)\) 의 시간 복잡도 비용이 듬.
- #bin이 #data보다 훨씬 더 작기 때문에, 히스토그램 구축이 계산 복잡도를 지배할 것임.
- #data 또는 #feature 를 줄일 수 있다면, GBDT 훈련을 상당히 가속화할 수 있을 것임.
2-2. Related Work
- GBDT를 구현한 것들이 꽤 있음.
- 이 중 XGBoost가 다른 것들 보다 좋은 성능을 내기 때문에, 이를 Baseline으로 사용함.
훈련 데이터 크기를 줄이기 위한 흔한 접근법은 데이터 인스턴스를 Down Sampling하는 것임.
- 예를 들어, 데이터 인스턴스 가중치가 고정된 임계값 (Threshold) 보다 작다면 이 인스턴스는 걸러짐.
- SGB (Stochastic Gradient Boosting) 은 모든 반복에서 무작위 Subset을 사용하여 약한 학습기를 훈련시킴.
- Sampling 비율은 훈련 진행 과정에서 동적으로 조정됨.
- 그러나, SGB를 제외한 이 모든 연구들은 AdaBoost를 기반으로 하며, GBDT에서 데이터 인스턴스에 대한 Native 가중치가 없기 때문에 GBDT를 직접 적용할 수 없음.
- SGB를 GBDT에 적용할 수 있지만, 보통 정확도에 해를 끼치기 때문에 올바른 선택이 아님.
이와 유사하게, Features 수를 줄이기 위해, 약한 Features를 거르는 것은 자연스러움.
- 여기서는 보통 PCA (Principle Component Analysis) 또는 Project Pursuit을 사용함.
- 그러나, 이러한 접근들은 Features가 상당한 중복성을 가진다는 가정에 매우 의존하지만, 이는 실제로 항상 참인 것은 아님 (Features는 보통 고유한 기여도를 가지고 설계되며, 그 중 어느 하나라도 제거하면 훈련 정확도에 어느 정도 영향을 미칠 수 있음).
보통 실제 어플리케이션에서 사용되는 대규모 데이터셋은 꽤 Sparse함.
- Pre-sorted 알고리즘 기반 GBDT는 값이 0인 Features를 무시하여 훈련 비용을 줄일 수 있음.
- 그러나, 히스토그램-기반 알고리즘 기반 GBDT는 효율적인 Sparse 최적화 솔루션을 가지고 있지 않음.
- 그 이유는 이 알고리즘이 Feature 값이 0이든 아니든 상관없이 각 데이터 인스턴스에 대해 Feature Bin 값을 검색해야 된다는 것임.
- 히스토그램-기반 알고리즘 기반 GBDT가 그러한 Sparse한 속성을 효과적으로 활용할 수 있다는 것 때문에 많이 선호됨.
- 이전 연구들의 한계점들을 다루기 위해, GOSS와 EFB라 부르는 새로운 기법들을 제안함.
3. Gradient-based One-Side Sampling
3-1. Algorithm Description
- AdaBoost에서, Sample 가중치는 데이터 인스턴스 중요도에 대한 좋은 지표 역할을 수행함.
- 그러나, GBDT에서, Native Sample 가중치가 없기 때문에, AdaBoost에 대해 제시된 Sampling 기법들을 직접 적용할 수 없음.
- 다행히, GBDT의 각 데이터 인스턴스 Gradient가 데이터 Sampling에 대해 유용한 정보를 제공함.
- 즉, 인스턴스가 작은 Gradient와 관련 있다면, 이 인스턴스의 훈련 오류는 작고, 이미 잘 훈련된 것임.
- 여기서 간단한 아이디어가 있는데, 작은 Gradients를 가진 데이터 인스턴스들을 버리는 것임.
- 하지만, 그렇게 하게 되면 데이터 분포가 변경되고, 학습된 모델 정확도에 해를 끼칠 것임.
- 이러한 문제를 피하기 위해, 우리는 GOSS (Gradient-based One-Side Sampling) 라는 새로운 방법을 제시함.
GOSS는 큰 Gradients를 가진 모든 인스턴스를 유지하고, 작은 Gradients를 가진 인스턴스를 무작위로 Sampling을 수행함.
- 데이터 분포에 미치는 영향을 보상하기 위해, Information Gain을 계산할 때, GOSS는 작은 Gradients를 가진 데이터 인스턴스에 대해 상수 Multiplier를 도입함 (Algorithm 2 참조).
- 구체적으로 애기하면 다음과 같이 진행함 :
- GOSS는 제일 먼저 데이터 인스턴스 Gradients의 절댓값에 따라 인스턴스를 정렬하고, Top \(a \, \times \, 100\)% 만큼 인스턴스를 선택함.
- 그런 다음, 나머지 데이터에서 \(b \, \times \, 100\)% 만큼 인스턴스를 무작위로 Sampling함.
- 그 이후에, GOSS는 Information Gain을 계산할 때, 상수 \(1-a\over b\) 를 가지고 작은 Gradients를 가진 Sampling된 데이터를 증폭시킴.
- 그렇게 하여, 초기 데이터 분포의 큰 변경 없이 덜 훈련된 인스턴스에 더 집중할 수 있음.
4. Exclusive Feature Bundling
- 보통 고차원 데이터는 매우 Sparse함.
- Feature 공간의 Sparsity는 Feature 수를 감소시키기 위해 거의 손실 없는 접근을 설계할 수 있는 가능성을 제공함.
- 구체적으로, Sparse Feature 공간에서, 많은 Features는 상호 배타적인 관계를 가짐 (즉, 이들이 0이 아닌 값을 동시에 가질 수 없음).
- 우리는 배타적인 Features를 단일 Feature로 안전하게 Bundle할 수 있음 (이를 \(Exclusive \, Feature \, Bundle\) 이라 부름).
- 신중하게 설계된 Feature Scanning 알고리즘에서, 우리는 Feature Bundles로, 개별 Features로 만든 Feature 히스토그램과 동일한 히스토그램을 구축할 수 있음.
- 이 방법으로, 히스토그램 구축 복잡성은 \(O(\#data \, \times \, \#feature)\) 에서 \(O(\#data \, \times \, \#bundle)\) 로 변경됨.
- \(\#bundle \, << \, \#feature\)
- 그렇게 되면, 정확도 손실 없이 GBDT의 훈련을 상당히 가속화할 수 있음.
- 두 개의 이슈를 다뤄 보겠음 :
- 어떤 Feature를 함께 Bundle해야 하는지를 결정.
- Bundle을 구축하는 방법.
Theorem 4.1 The problem of partitioning features into a smallest number of exclusive bundles is NP-hard.
- Proof :
- 우리는 우리의 문제를 그래프 Coloring 문제로 감소시킬 것임.
- 그래프 Coloring 문제가 NP-hard이기 때문에, 우리는 결론을 추론할 수 있음.
- 그래프 Coloring 문제의 어떤 인스턴스 \(G \, = \, (V, E)\) 가 주어졌다고 해보겠음.
- 우리는 다음과 같이 인스턴스를 구축함 :
- Incidence 행렬 \(G\) 의 각 Row를 Feature로 취함.
- 그리고 |\(V\)| 개의 Features를 가진 인스턴스를 얻음.
- 배타적인 Features Bundle이 동일한 Color를 가진 Vertices의 집합에 해당한다는 것을 쉽게 알 수 있으며, 반대의 경우도 마찬가지임.
이슈 (1) : 어떤 Feature를 함께 Bundle해야 하는지를 결정
- 우리는 최적 Bundling 전략을 찾는 것이 NP-Hard라는 사실을 Theorem 4.1을 증명함.
- NP-Hard는 다항 시간 (Polynomial Time) 내에 정확한 솔루션을 찾는 것이 불가능 하다는 것을 나타냄.
- 좋은 근사 알고리즘을 찾기 위해 다음과 같이 수행함 :
- 우리는 먼저 Features를 Vectics로 취하여 최적 Bundling 문제를 그래프 Coloring 문제로 감소시킴.
- 상호 배타적이지 않은 모든 Feature Pair에 대해서만 Edges를 추가함.
- Bundles를 만들기 위해 그래프 Coloring에 대해 합리적으로 좋은 결과 (상수 근사 비율을 이용) 를 낼 수 있는 탐욕 알고리즘을 사용함.
- 간단히 계산하여, Feature 값의 작은 부분을 무작위로 Polluting 하는 것은 훈련 정확도에 최대 \(O([(1-\gamma)n]^{-2/3})\) 까지 영향을 미칠 것임.
- \(\gamma\) : 각 Bundle 의 최대 Conflict 비율임.
- 그래서, 우리가 상대적으로 작은 \(\gamma\) 를 선택하면, 정확도와 효율성 사이의 좋은 균형을 얻을 수 있을 것임.
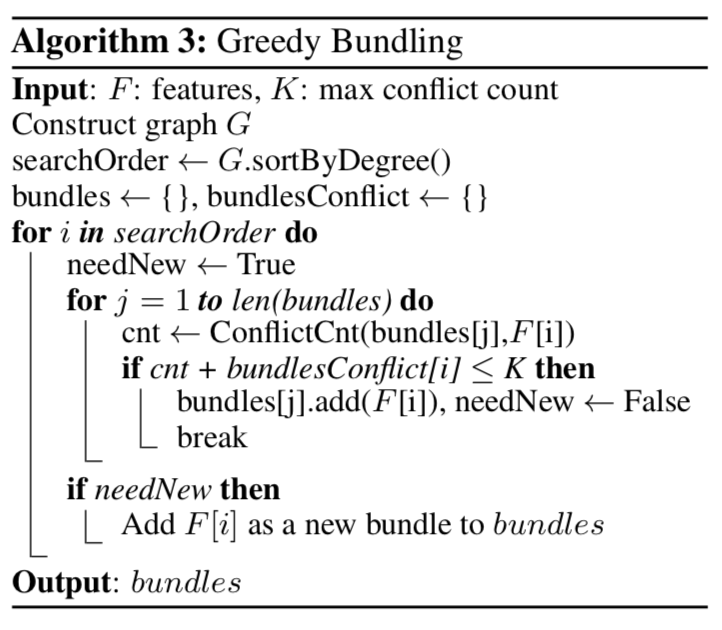
- 위 논의를 바탕으로, 우리는 Algorithm 3과 같이 배타적인 Feature Bundling에 대한 알고리즘을 설계함.
- 첫 번째로, 가중치가 적용된 Edges를 이용하여 그래프를 구축함.
- 이 가중치들은 Features 사이의 전체 Conflicts에 해당함.
- 두 번째로, 그래프의 Features Degrees로 Features를 내림차순 정렬함.
- 마지막으로, 정렬된 리스트에서 각 Feature를 확인하고, 작은 Conflict (\(\gamma\) 로 조절) 를 가진 기존 Bundle에 Feature를 할당하거나, 새로운 Bundle을 만듬.
- 첫 번째로, 가중치가 적용된 Edges를 이용하여 그래프를 구축함.
- Algorithm 3의 시간 복잡도는 \(O(\#feature^{2})\) 이고, 훈련 전에 한 번만 진행됨.
- 이 복잡도는 Features 수가 매우 크지 않을 때는 허용 가능하지만, Feature 수가 수백만 개라면 여전히 어려움을 겪을 수 있음.
- 효율성을 더 향상시키기 위해, 그래프 구축 없이 더 효율적인 정렬 전략을 제시함 :
- 0이 아닌 값의 개수로 정렬.
- 이는 0이 아닌 값이 Conflict 확률을 더 높게 만들기 때문에 Degrees로 정렬하는 것과 유사함.
이슈 (2) : Bundle을 구축하는 방법
- 훈련 복잡도를 줄이기 위해, 동일한 Bundle의 Features를 병합하는 좋은 방법이 필요함.
- 핵심은 Feature Bundles에서 원래 Feature 값을 식별할 수 있는지 확인하는 것임.
- 히스토그램-기반 알고리즘은 연속적인 Feature 값 대신 이산적인 Bins를 저장하기 때문에, 우리는 서로 다른 Bins에 배타적인 Features를 넣어서 Feature Bundle을 구축할 수 있음.
- 이는 초기 Feature 값에 Offsets를 추가하여 수행할 수 있음.
- 예를 들어, Feature Bundle에 두 개의 Features를 가지고 있다고 가정하겠음.
- Feature A 는 [0, 10), Feature B는 [0, 20)의 값을 취함.
- 그런 다음, 개선된 Feature가 [10, 30)에서 값을 취하도록 Feature B 값에 Offset 10을 더함.
- 그 이후에는 Feature A & B를 합병하는 것이 안전하며, 범위 [0, 30] 을 가진 Feature Bundle을 원래 Features A & B 대신 사용함.
- Algorithm 4에 설명되어 있음.

- EFB 알고리즘은 많은 수의 배타적인 Features를 훨씬 더 적은 수의 Dense Feature로 Bundle할 수 있으며, 이는 값이 0인 Feature에 대해 불필요한 계산을 효과적으로 피할 수 있음.
- 실제로, 우리는 0이 아닌 값을 가진 데이터가 기록된 각 Feature 테이블을 사용하여, 값이 0인 Feature를 무시하는 방향으로 기본 히스토그램-기반 알고리즘도 최적화할 수 있음.
- 이 테이블 데이터를 조사함으로써, Feature에 대한 히스토그램 구축 비용은 \(O(\#data)\) 에서 \(O(\#non_zero_data)\) 로 바뀔 것임.
- 그러나, 이 방법은 전체 트리 성장 과정에서 이러한 Feature 별 테이블을 유지하기 위해 추가적인 메모리와 계산 비용이 필요함.
- 우리는 LightGBM에 이 최적화를 기본 함수로 구현함.
- 이 최적화가 Bundles이 Sparse할 때도 여전히 사용할 수 있기 때문에, EFB와 충돌하지 않는 다는 것에 주목해야 함.
6. Conclusion
- 이 논문에서, 우리는 새로운 GBDT 알고리즘인 LightGBM을 제시했음.
- 이는 두 개의 새로운 기법들을 포함하고 있음 :
- GOSS \((Gradient\-based \, One\-Side \, Sampling)\) : 대규모 데이터 인스턴스를 다루기 위한 것.
- EFB \((Exclusive \, Feature \, Bundling)\) : 대규모 Features 수를 다루기 위한 것.
- 이는 두 개의 새로운 기법들을 포함하고 있음 :
- 이러한 두 가지 기법들에 대해 이론적인 분석과 실험 연구들을 수행했음.
- 실험 결과는 이론과 일치했고, GOSS와 EFB을 이용하여, LightGBM이 계산 속도와 메모리 사용면에서 XGBoost와 SGB보다 상당히 좋은 성능을 낼 수 있는 것을 보여줌.
- 추후의 연구에서, 우리는 GOSS의 \(a\) 와 \(b\) 의 최적의 선택을 연구할 것이며, Feature가 Sparse하든 아니든 상관없이 대규모 Feature를 다루기 위해 EFB의 성능을 지속적으로 향상시킬 것임.
반응형
'Paper > ML (Machine Learning)' 카테고리의 다른 글
댓글
