티스토리 뷰
NLP (Natural Language Processing)
NPLM (Neural Probabilistic Language Model)
기내식은수박바 2020. 1. 18. 01:11반응형
기존 통계 기반 언어 모델의 문제점
- 학습 데이터에 존재하지 않는 n-gram 데이터가 포함된 문장이 나타날 확률 값을 0으로 부여한다.
- 이러한 문제점은 Back-off 또는 Smoothing 방법으로 일부 보완할 수는 있지만 완전히 해결할 수 있는 것은 아니다.
- '장기 의존성 (Long-Term Dependency)' 문제가 발생한다.
- 즉, n-gram 의 n 의 값이 커질수록 등장 확률 값이 0인 단어 시퀀스가 폭발적으로 증가하게 된다.
- 단어 / 문장 간 유사도를 계산할 수 없다.
- 단어들은 모두 원-핫 벡터로 표현되고, 두 단어의 유사성을 구하기 위해 내적을 할 경우 값은 항상 0이 나오며, 이는 두 단어 벡터가 직교 (Orthogonal) 한다는 것이다.
- 직교한다는 것은 두 벡터가 서로 독립적 (Independent) 이라는 것을 의미하지만, 현실에서는 단어들간 관련성이 없는 것이 아니다.
- 이러한 문제를 해결하기 위해 분산 표현 (Distributed Representation) 이라는 개념이 등장한다.
- 분산 표현 : Distributed Representation
Back-off ?
- n-gram 등장 빈도를 n보다 작은 범위의 단어 시퀀스로 근사하는 방식이다.
- ex) "나는 친구와 저녁에 방탈출 카페에서 방탈출을 하였다" 라는 문장이 있으며, 말뭉치에 한 번도 등장하지 않아 확률이 0이라고 해보자.
- 7-gram 모델을 적용하면 당연히 등장 확률이 0으로 나오게 될 것이다.
- Back-off 방식을 이용하여 7 을 4 (원하는 숫자) 로 줄인 다음 근사한 수식은 아래와 같을 것이다.
- α와 β는 실제 빈도와의 차이를 보정해주는 파라미터이다.
- 빈도가 1 이상이면 Back-off 방식을 사용할 필요 없이 그 빈도를 그대로 사용하면 된다.

Smoothing
- 등장 빈도 표에 모두 k만큼 빈도수를 더해주는 기법이다.
- "나는 친구와 저녁에 방탈출 카페에서 방탈출을 하였다" 라는 문장의 빈도는 k = (0 + k) 될 것이며, Add + k Smoothing 이라고도 한다.
- Smoothing을 수행하면 등장 빈도가 높은 단어들의 등장 확률을 일부 깎고, 등장하지 않은 단어들에는 일부 확률을 부여한다.
NPLM (Neural Probabilistic Language Model) ?
- NPLM은 통계 기반 언어 모델 문제점을 일부 극복한 방법이며, 아키텍처는 아래와 같다.
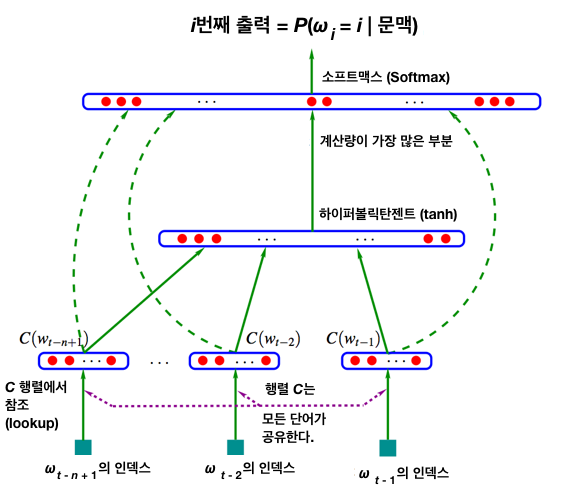
NPLM의 학습 과정
- NPLM은 n - 1개의 단어 시퀀스를 가지고 n번째 단어를 예측하는 n-gram 언어 모델이다.
- 즉, 단어 시퀀스가 주어지고 다음 단어가 무엇인지 맞추는 과정에서 학습한다.
- NPLM은 아래 수식을 최대화 하려고 하며, 각 조건부 확률 \(P\) (\(w_{4}\) | \(w_{1}\), \(w_{2}\), \(w_{3}\)), \(P\) (\(w_{5}\) | \(w_{2}\), \(w_{3}\), \(w_{4}\)), \(...\) 을 높인다는 의미이다.

수식 설명
- \(w_{t}\) : \(t\) 번째 단어
- \(y_{w_{t}}\) : '출력 (Output)' 부분에서 설명
입력 (Input)
- 아래 수식을 통해 문장 내 \(t\) 번째 단어 \(w_{t}\) (원-핫 벡터로 되어 있다) 에 대응하는 단어 벡터 \(x_{t}\) 를 만든다.
$$x_{t} = C (w_{t})$$
- \(|V|\) x \(m\) 크기를 갖는 커다란 행렬 \(C\) 에서 \(w_{t}\) 에 해당하는 벡터를 참조 (Lookup) 한 형태이다.
- \(C\) 행렬의 초기 원소 값은 랜덤으로 초기화한다.
- \(|V|\) 는 어휘 집합 크기, \(m\) 은 \(x_{t}\) 의 차원 수다.
- 이렇게 나온 문장 내 모든 단어에 대한 벡터 \(x_{t}\) 를 이어붙인다 (Concatenate).
참조 (Lookup) ?
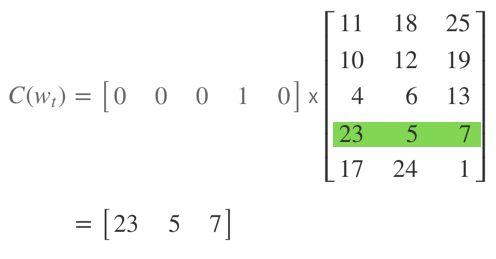
- 어휘 집합에 속한 단어가 5개 뿐이고, \(w_{t}\)가 네 번째 단어라고 가정하자.
- 그러면 \(C(w_{t})\) 는 행렬 \(C\)와 \(w_{t}\) 에 해당하는 원-핫 벡터 (One-hot Vector) 를 내적 (Inner Product) 한 것과 같다.
- 이는 \(C\) 행렬에서 \(w_{t}\) 에 해당하는 행 (Row) 만 참조하는 것과 동일하다.
출력 (Output)
- NPLM은 \(|V|\) 차원의 Score 벡터 \(y_{w_{t}}\) 에 Softmax 함수를 적용한 \(|V|\) 차원의 확률 벡터를 출력으로 내놓는다.
- 이는 곧 조건부 확률과 같으며, 확률 벡터에서 가장 높은 요소의 인덱스에 해당하는 단어가 실제 정답 단어와 일치하도록 학습한다.
입력부터 출력 사이의 과정
- 행렬 \(C\) 를 참조하여 단어 \(w\) \(=\) [\(w_{t - 1}\), \(w_{t - 2}\), \(...\), \(w_{t - n + 1}\)] 를 단어 벡터 \(x\) \(=\) [\(x_{t - 1}\), \(x_{t - 2}\), \(...\), \(x_{t - n + 1}\)] 로 만들었다.
- 그 다음 n - 1 개의 단어 벡터 \(x\) \(=\) [\(x_{t - 1}\), \(x_{t - 2}\), \(...\), \(x_{t - n + 1}\)] 와 아래 수식을 이용하여 \(y_{w}\) 를 계산한다.
$$y_{w_{t}} = b + U · tanh(d + Hx_{t})$$
- 마지막으로 각 \(y_{w_{t}}\) 에 Softmax 함수를 적용한 뒤 이를 정답 단어의 인덱스와 비교하여 역전파 (Backpropagation) 방식으로 학습이 이루어진다.
- 최종적으로 학습이 종료되면 행렬 \(C\) 를 각 단어에 해당하는 \(m\) 차원 임베딩으로 사용한다.
- 다음은 NPLM의 파라미터 차원 수를 정리한 것이다.
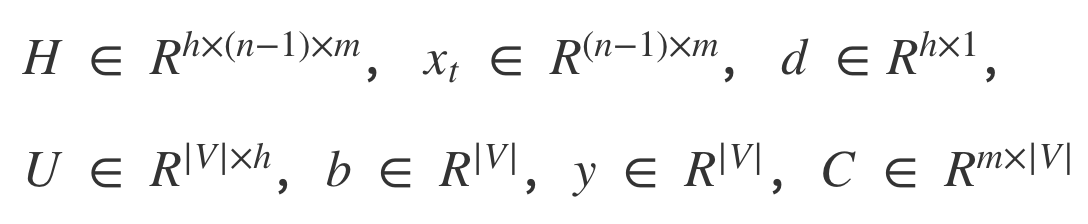
의미 정보
- ["나는", "친구와", "저녁에"] 단어들을 가지고 "방탈출" 이라는 단어를 맞추는 과정에서 생기는 학습 손실을 최소화하는 그래디언트 (Gradient) 를 받아 동일하게 업데이트 된다.
- 이는 단어 벡터들이 벡터 공간에서 같은 방향으로 조금씩 움직인다고 볼 수 있다.
- 결과적으로 임베딩 벡터 공간상에서 거리가 가깝다는 것은 의미가 유사하다는 것이다.
NPLM의 이점과 한계
- 기존 통계적 n-gram 언어 모델을 일부 개선하였지만 여전히 문제점을 가지고 있다.
1) 기존 모델에서의 개선점 (One-hot Vector -> Distributed Representation / Sparse -> Dense)
- NPLM은 밀집 벡터 (Dense Vector) 를 사용한다.
- 이 밀집 벡터를 통해 단어의 유사도를 표현할 수 있으며, 희소성 문제 (Sparsity Problem) 를 해결할 수 있다.
- 또한, 모든 n-gram을 저장하지 않기 때문에 n-gram 언어 모델보다 저장 공간의 이점을 가진다.
2) 고정된 길이 입력 (Fixed-length input)
- NPLM은 n-gram 언어 모델과 마찬가지로 다음 단어를 예측하기 위해 이전의 모든 단어를 참고하는 것이 아닌, 정해진 n개의 단어만 참고한다.
- 이는 버려진 단어들의 문맥 정보를 참고할 수 없다는 것이다.
- 훈련 말뭉치에 있는 각 문장의 길이가 전부 다를 수 있으며, 이를 개선하기 위해서는 모델이 매번 다른 길이의 입력 시퀀스에 대해서도 처리할 수 있는 능력이 있어야 한다.
3) 계산복잡성 (Computational Complexity)
- 임베딩으로 사용하는 행렬 \(C\) 외에도 \(H\), \(U\), \(b\), \(d\) 등 다른 파라미터들까지 업데이트를 해줘야 한다.
- 따라서, 과적합 (Overfitting) 이 발생할 위험이 높다.
- 이러한 문제점을 극복하기 위해 학습 파라미터를 줄이는 방향으로 제시된 모델이 Word2Vec이다.
Reference
- https://mc.ai/자연어처리nlp-nplm/
- https://wikidocs.net/45609
- https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/03/29/NNLM/
- 도서 : 한국어 임베딩 (저 : 이기창)
논문
반응형
'NLP (Natural Language Processing)' 카테고리의 다른 글
| LSTM (Long Short Term Memory) (0) | 2019.11.15 |
|---|---|
| RNN (Recurrent Neural Network) (0) | 2019.11.15 |
| Distributed Representation / Dense Vector (0) | 2019.03.28 |
댓글
