티스토리 뷰
반응형

문제
- 동물원에서 막 탈출한 원숭이 한 마리가 세상구경을 하고 있다.
- 그러다가 평화로운 마을에 가게 되었는데, 그곳에서는 알 수 없는 일이 벌어지고 있었다.
- 마을은 N개의 집과 그 집들을 연결하는 M개의 길로 이루어져 있다.
- 길은 어느 방향으로든지 다닐 수 있는 편리한 길이다.
- 그리고 각 길마다 길을 유지하는데 드는 유지비가 있다.
- 마을의 이장은 마을을 두 개의 분리된 마을로 분할할 계획을 가지고 있다.
- 마을이 너무 커서 혼자서는 관리할 수 없기 때문이다.
- 마을을 분할할 때는 각 분리된 마을 안에 집들이 서로 연결되도록 분할해야 한다.
- 각 분리된 마을 안에 있는 임의의 두 집 사이에 경로가 항상 존재해야 한다는 뜻이다.
- 마을에는 집이 하나 이상 있어야 한다.
- 그렇게 마을의 이장은 계획을 세우다가 마을 안에 길이 너무 많다는 생각을 하게 되었다.
- 일단 분리된 두 마을 사이에 있는 길들은 필요가 없으므로 없앨 수 있다.
- 그리고 각 분리된 마을 안에서도 임의의 두 집 사이에 경로가 항상 존재하게 하면서 길을 더 없앨 수 있다.
- 마을의 이장은 위 조건을 만족하도록 길들을 모두 없애고 나머지 길의 유지비의 합을 최소로 하고 싶다.
- 이것을 구하는 프로그램을 작성하시오.
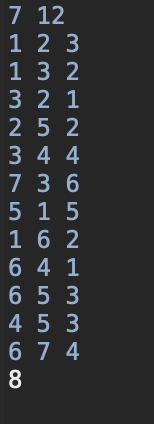
입력
- 첫째 줄에 집의 개수 N, 길의 개수 M이 주어진다.
- N은 2이상 100,000이하인 정수이고, M은 1이상 1,000,000이하인 정수이다.
- 그 다음 줄부터 M줄에 걸쳐 길의 정보가 A B C 세 개의 정수로 주어지는데 A번 집과 B번 집을 연결하는 길의 유지비가 C (1 ≤ C ≤ 1,000)라는 뜻이다.
출력
- 첫째 줄에 없애고 남은 길 유지비의 합의 최솟값을 출력한다.

솔루션
- 최소 스패닝 트리 (MST) 를 이용한 문제이다.
- 이 문제에서는 크루스칼을 이용하여 풀었다.
- 크루스칼은 Disjoint Set을 바탕으로 이루어졌다.
- 문제의 조건인 집들을 2개의 마을로 분할해야 된다는 것을 고려해야 한다.
- MST는 N개의 집이 있을 때, 가중치가 적은 N - 1개의 길을 통해 모든 집을 연결하는 알고리즘이다.
- 여기서 마지막에 합류되는 길을 연결하지 않는다면 N - 2개의 길을 이용할 것이고, 두 개의 마을로 나누어질 것이다.
- 아래 그림 예시를 통해 확인해보자.
예시

Code
- 전체 코드 : Solution_1647
초기에 각 노드의 루트 노드를 본인으로 초기화하는 함수
|
1
2
3
4
|
public static void Initialize() {
for (int i = 1; i <= N; i++)
parent[i] = i;
}
|
cs |
노드가 속한 집합의 루트 노드를 찾는 함수
|
1
2
3
4
5
6
|
public static int Find(int u) {
if (parent[u] == u)
return u;
return parent[u] = Find(parent[u]);
}
|
cs |
두 노드 집합을 합치는 합집합 연산 함수
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
public static void Union(int u, int v) {
int uR = Find(u);
int vR = Find(v);
if (uR == vR)
return;
if (rank[uR] > rank[vR])
Swap(uR, vR);
parent[uR] = vR;
if (rank[uR] == rank[vR])
rank[vR]++;
}
|
cs |
간선 객체를 생성하는 클래스 (우선순위 큐를 사용하기 위한 오버라이딩)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public static class Edge implements Comparable<Edge> {
int x, y, cost;
public Edge(int x, int y, int cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
@Override
public int compareTo(Edge e) {
return this.cost - e.cost;
}
}
|
cs |
크루스칼 알고리즘이 동작하는 함수
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public static int Kruskal() {
int mcost = 0;
int count = 0;
while (count < N - 2) {
Edge edge = edgelist.poll();
if (Find(edge.x) != Find(edge.y)) {
mcost += edge.cost;
count++;
Union(edge.x, edge.y);
}
}
return mcost;
}
|
cs |
메인 함수
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
parent = new int[N + 1];
rank = new int[N + 1];
edgelist = new PriorityQueue<>();
Initialize();
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
edgelist.offer(new Edge(from, to, cost));
}
bw.write(Kruskal() + " ");
bw.flush();
bw.close();
br.close();
}
|
cs |
결과
반응형
'Algorithm > Solution' 카테고리의 다른 글
| [프로그래머스] - 정수 삼각형 (0) | 2020.03.16 |
|---|---|
| [백준 6497] - 전력난 (0) | 2020.03.16 |
| [백준 10774] - 저지 (0) | 2020.03.12 |
| [백준 10775] - 공항 (0) | 2020.03.12 |
| [백준 4195] - 친구 네트워크 (0) | 2020.03.12 |
댓글
