티스토리 뷰
Algorithm/Technique
최소 스패닝 트리 (MST, Minimum Spanning Tree) : 크루스칼 (Kruskal)
기내식은수박바 2019. 12. 10. 02:11반응형
스패닝 트리 (Spanning Tree) ?
- 그래프의 정점 전부와 간선의 부분 집합으로 구성된 부분 그래프이다.
- 아래와 같은 예시들이 스패닝 트리라고 할 수 있다.
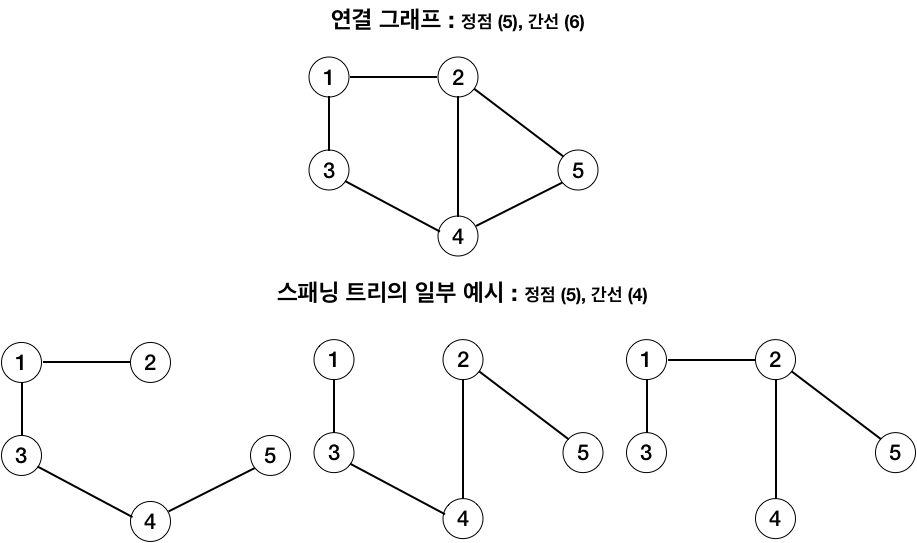
- 스패닝 트리에 포함된 간선들은 정점들을 트리 형태로 전부 연결해야 한다.
- 또한, 트리 형태여야 한다는 말은 선택된 간선이 사이클을 이루지 않는다는 의미여, 정점들이 부모-자식 관계로 연결될 필요는 없다는 것이다.
최소 스패닝 트리 (MST, Minimum Spanning Tree) ?
- 가중치 그래프의 스패닝 트리 중 가중치의 합이 가장 작은 트리이다.
- 최소 스패닝 트리를 구할 수 있는 알고리즘은 두 가지가 있다.
- 크루스칼 (Kruskal) 알고리즘
- 프림 (Prim) 알고리즘 : Prim Algorithm
크루스칼 (Kruskal) 알고리즘
- 크루스칼 알고리즘은 가중치가 작은 간선이 최소 스패닝 트리에 포함될 가능성이 높다는 것에서 출발한다.
- 먼저 그래프의 모든 간선을 가중치의 오름차순으로 정렬한다.
- 스패닝 트리에 간선을 하나씩 추가한다.
- 여기서 간선의 가중치가 작다고 해서 무조건 트리에 더하면 안된다.
- Why ? - 선택한 간선들이 사이클을 이룰 수 있기 때문에, 따라서 사이클이 생기는 간선은 고려에서 제외해야 한다.
- 이렇게 모든 간선을 한 번씩 검사하고 난 뒤 종료한다.
과정
- 크루스칼 알고리즘의 과정은 아래와 같다.
- 아래 그림에서 눈여겨봐야할 점은 Roop 4 -> 5로 넘어가는 과정이다.
- 남아있는 두 개의 가중치 3인 간선을 추가하면 사이클이 형성되며, 이는 더이상 트리가 아니게 된다.
- 따라서, 가중치 4인 간선을 추가한다.

- 크루스칼 알고리즘은 상호-배타 집합 (Disjoint Set) 의 Union-Find 알고리즘을 이용한다.
- 이 구조에서 한 집합은 그래프의 한 컴포넌트를 표현한다.
- 따라서 그래프에 새 간선을 추가해 사이클이 생기는지를 확인하려면 두 정점이 이미 같은 집합에 속해 있는지를 확인하면 되고, 간선을 트리에 추가할 경우에는 이들이 포함된 두 집합을 합치면 된다.
특징
- Disjoint Set에 대한 연산은 상수 시간이나 다름 없기 때문에 실제 트리를 만드는 for문 시간 복잡도는 O(|E|) 이다.
- 따라서 전체 시간 복잡도는 간선 목록의 정렬에 걸리는 시간 O(E * log E) 을 가진다.
- 크루스칼 알고리즘은 각 간선을 그래프에 추가할 때 뒤에 오는 간선들에 대한 고려는 전혀 하지 않기 때문에 탐욕 알고리즘이라 할 수 있다.
- 또한, 노드의 수가 많고 간선의 수가 적은 그래프에서 알고리즘 효율이 올라간다.
Code
그래프를 형성하는 Graph 클래스
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Graph {
int V; // 정점의 갯수
List<Edge> edgelist; // 간선 리스트
Subset[] subset; // 각 정점이 속한 트리 부분집합
public Graph(int size) {
this.V = size + 1;
edgelist = new ArrayList<>();
subset = new Subset[this.V];
for (int i = 1; i < this.V; i++)
subset[i] = new Subset(i, 0); // 초기에는 부분집합에 본인 정점만
}
// 간선 정보를 추가하는 함수
public void AddEdge(int x, int y, int cost) {
edgelist.add(new Edge(x, y, cost));
}
}
|
간선 정보를 담는 Edge 클래스
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Edge implements Comparable<Edge> {
int x, y, cost;
public Edge(int x, int y, int cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
@Override // cost를 기준으로 오름차순 정렬을 위한 함수 오버라이딩
public int compareTo(Edge e) {
return this.cost - e.cost;
}
}
|
부분집합 트리 정보를 담는 SubSet 클래스
|
1
2
3
4
5
6
7
8
|
class Subset {
int parent, rank;
public Subset(int parent, int rank) {
this.parent = parent; // 루트노드
this.rank = rank; // 트리높이
}
}
|
u가 속한 트리의 루트노드의 번호를 반환하는 함수
|
1
2
3
4
5
6
|
public static int Find(int u) {
if (graph.subset[u].parent == u)
return u;
else
return graph.subset[u].parent = Find(graph.subset[u].parent);
}
|
u가 속한 트리와 v가 속한 트리를 합치는 함수
- 항상 높이가 더 낮은 트리를 더 높은 트리밑에 집어넣음으로써 트리의 높이가 높아지는 상황을 방지하는 것이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
public static void Union(int u, int v) {
int uR = Find(u);
int vR = Find(v);
if (uR == vR)
return;
if (graph.subset[uR].rank > graph.subset[vR].rank)
Swap(uR, vR);
graph.subset[uR].parent = vR;
if (graph.subset[uR].rank == graph.subset[vR].rank)
graph.subset[vR].rank++;
}
|
크루스칼 알고리즘을 수행하는 Kruskal 함수
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public static void Kruskal() {
Collections.sort(graph.edgelist); // 간선 오름차순 정렬
Edge[] result = new Edge[graph.V];
int mst = 0, idx = 1;
for (int i = 0; i < graph.edgelist.size(); i++) {
Edge edge = graph.edgelist.get(i);
if (Find(edge.x) != Find(edge.y)) { // 간선의 양 끝 정점의 루트노드가 다르다면
Union(edge.x, edge.y); // 두 정점은 다른 부분집합 트리에 있으므로 합친다.
mst += edge.cost;
result[idx++] = edge;
}
}
for (int i = 1; i < idx; i++)
System.out.println(result[i].x + " - " + result[i].y +
" cost : " + result[i].cost);
System.out.println("MST : " + mst);
}
|
전체 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
|
import java.util.*;
import java.io.*;
public class test1 {
static Graph graph;
public static void Swap(int n1, int n2) {
int temp = n1;
n1 = n2;
n2 = temp;
}
public static void Union(int u, int v) {
int uR = Find(u);
int vR = Find(v);
if (uR == vR)
return;
if (graph.subset[uR].rank > graph.subset[vR].rank)
Swap(uR, vR);
graph.subset[uR].parent = vR;
if (graph.subset[uR].rank == graph.subset[vR].rank)
graph.subset[vR].rank++;
}
public static int Find(int u) {
if (graph.subset[u].parent == u)
return u;
else
return graph.subset[u].parent = Find(graph.subset[u].parent);
}
public static void Kruskal() {
Collections.sort(graph.edgelist);
Edge[] result = new Edge[graph.V];
int mst = 0, idx = 1;
for (int i = 0; i < graph.edgelist.size(); i++) {
Edge edge = graph.edgelist.get(i);
if (Find(edge.x) != Find(edge.y)) {
Union(edge.x, edge.y);
mst += edge.cost;
result[idx++] = edge;
}
}
for (int i = 1; i < idx; i++)
System.out.println(result[i].x + " - " + result[i].y +
" cost : " + result[i].cost);
System.out.println("MST : " + mst);
}
public static void main(String[] args) {
graph = new Graph(9);
graph.AddEdge(1, 2, 4);
graph.AddEdge(2, 3, 8);
graph.AddEdge(3, 4, 7);
graph.AddEdge(4, 5, 9);
graph.AddEdge(5, 6, 10);
graph.AddEdge(6, 7, 2);
graph.AddEdge(7, 8, 1);
graph.AddEdge(8, 9, 7);
graph.AddEdge(1, 8, 8);
graph.AddEdge(2, 8, 11);
graph.AddEdge(3, 6, 4);
graph.AddEdge(3, 9, 2);
graph.AddEdge(4, 6, 14);
graph.AddEdge(7, 9, 6);
Kruskal();
}
}
class Graph {
int V; // 정점의 갯수
List<Edge> edgelist; // 간선 리스트
Subset[] subset; // 각 정점이 속한 트리 부분집합
public Graph(int size) {
this.V = size + 1;
edgelist = new ArrayList<>();
subset = new Subset[this.V];
for (int i = 1; i < this.V; i++)
subset[i] = new Subset(i, 0); // 초기에는 부분집합에 본인 정점만
}
// 간선 정보를 추가하는 함수
public void AddEdge(int x, int y, int cost) {
edgelist.add(new Edge(x, y, cost));
}
}
class Edge implements Comparable<Edge> {
int x, y, cost;
public Edge(int x, int y, int cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
@Override // cost를 기준으로 오름차순 정렬을 위한 함수 오버라이딩
public int compareTo(Edge e) {
return this.cost - e.cost;
}
}
class Subset {
int parent, rank;
public Subset(int parent, int rank) {
this.parent = parent; // 루트노드
this.rank = rank; // 트리높이
}
}
|
반응형
'Algorithm > Technique' 카테고리의 다른 글
| 네트워크 유량 (Network Flow) (0) | 2020.03.24 |
|---|---|
| 최소 스패닝 트리 (MST, Minimum Spanning Tree) : 프림 (Prim) (0) | 2019.12.10 |
| 소수 (Prime Number) & 에라토스테네스의 체 (Eratosthenes's Sieve) (0) | 2019.12.05 |
| KMP (Knuth–Morris–Pratt) (0) | 2019.11.26 |
| 벨만-포드 (Bellman-Ford) (0) | 2019.11.17 |
댓글
