티스토리 뷰
Algorithm/Technique
DFS (Depth-First Search) & BFS (Breadth-First Search)
기내식은수박바 2019. 10. 8. 14:51반응형
그래프 탐색 (Graph Search) ?
- 하나의 정점 (Vertex) 에서 시작하여 간선 (Edge) 을 따라 차례대로 모든 정점들을 한 번씩 방문하는 것.
그래프를 탐색하는 두 가지 방법
- DFS (Depth-First Search)
- BFS (Breadth-First Search)

DFS (Depth-First Search)
- 깊이 우선 탐색이라고 하며, 해당 노드의 자식들을 모두 탐색한 후 다른 형제 노드를 탐색한다.
- 즉, 넓게 (Wide) 탐색하는 것이 아닌 깊게 (Deep) 탐색하는 것이다.
- 보통, 모든 노드를 방문하고자 할 때 사용한다.
- 자기 자신을 호출하는 순환 알고리즘 형태를 가지므로, 스택 (Stack) 혹은 재귀함수 (Recursive Function) 로 구현한다.
DFS 특징
- 전위 (Pre-Order), 중위 (In-Order), 후위 (Post-Order) 등의 트리 순회는 모두 DFS의 한 종류이다.
- 주의할 점은 노드를 방문했는지의 여부를 검사해야 한다. (그렇지 않으면 무한루프에 빠질 수 있다.)
- BFS보다는 좀 더 간단하게 코드를 작성할 수 있다.
- 모든 노드를 탐색하기 때문에 단순 검색 자체는 BFS에 비해 느리다.
DFS 시간 복잡도 (Time Complexity)
인접리스트 : O(|V| + |E|) (정점의 개수 : V, 간선의 개수 : E)
- 한 번 방문한 지점은 다시 방문하지 않는다.
- 하나의 정점에서 다음으로 방문할 다른 정점들을 순회하는 횟수가 그 정점의 차수 (간선의 개수) 와 같기 때문이다.
인접행렬 : O(V^2) (정점의 개수 : V)
- DFS() 를 호출하는 횟수는 |V| 번이다.
- 다음에 방문할 정점을 찾을 때 모든 정점을 순회하며 두 정점이 연결되어 있는지 확인해야 하기 때문이다.
DFS 과정
- 노드 0 (시작 정점) 을 방문한다.
- 방문했다고 표시한다.
- 노드 0과 인접한 노드들을 차례로 순회한다.
- 노드 0과 인접한 노드가 없다면 종료한다.
- 노드 0과 인접한 노드 1을 방문했다면, 0과 인접한 또 다른 노드를 방문하기 전에 노드 1과 인접한 노드들을 모두 방문해야 한다.
- 노드 1을 시작 정점으로 두고 다시 DFS를 수행하여, 1과 인접한 노드를 방문한다.
- 노드 1의 분기 (Branch) 를 전부 탐색하였다면, 다시 노드 0와 인접한 노드들 중 방문하지 않은 노드를 방문한다.
- 즉, 노드 1의 분기를 모두 완료해야 노드 0의 다른 인접한 노드를 탐색할 수 있다는 것이다.
- 방문 하지 않은 노드가 없다면 종료하고, 있다면 방문 하지 않은 노드를 시작 정점으로 하여 DFS를 수행한다.

BFS (Breadth-First Search)
- 넓이 우선 탐색이라고 한다.
- DFS와는 달리 현재 정점에서 갈 수 있는 모든 정점들을 탐색한 후, 탐색한 정점들에서 갈 수 있는 정점들을 탐색한다.
- 즉, 인접한 노드들을 먼저 탐색하는 것이다.
- BFS는 큐 (Queue) 로 구현한다.
BFS 특징
- 최단거리 경로를 찾을 때 사용한다.
- DFS와 마찬가지로 노드를 방문했는지의 여부를 체크해야 한다.
- DFS 보다는 구현이 좀 더 복잡하다.
- BFS는 재귀적으로 동작하지 않는다.
BFS 시간 복잡도
- DFS와 마찬가지로 똑같다.
- 모든 정점을 한 번씩 방문하며, 정점을 방문할 때마다 인접한 간선을 모두 검사하기 때문이다.
- 따라서, 인접 리스트의 경우 O(|V| + |E|), 인접 행렬의 경우 O(V^2) 의 시간 복잡도를 가진다.
BFS 과정
- 노드 0을 방문한다. (방문 체크)
- 큐 (Queue) 에 방문한 노드를 집어넣는다. (Enqueue)
- 초기 상태의 큐는 시작 노드만 저장한다.
- 즉, 노드 0과 인접한 이웃 노드들을 모두 방문한 다음에, 인접 이웃 노드들의 이웃 노드들을 방문한다.
- 큐에서 꺼낸 노드와 인접한 노드들을 모두 차례대로 방문한다.
- 큐에서 노드를 꺼낸 후 방문한다. (Dequeue)
- 큐에서 꺼낸 노드와 인접한 노드들을 모두 방문한다.
- 인접한 노드가 있다면 큐에 삽입한다. (Enqueue)
- 큐가 빌때까지 BFS 과정을 수행한다.

Code
- 아래의 코드는 모두 인접행렬을 바탕으로 짰다.
- DFS의 경우, 구현할 수 있는 방법은 두 가지가 있다.
- 재귀 (Recursion)
- 스택 (Stack)
- BFS의 경우, 구현할 수 있는 방법은 한 가지 이다.
- 큐 (Queue)
- 문제 유형 또한 두 가지로 나눌 수 있다.
- 맵 (Map)
- 그래프 (Graph)
선행으로 구현 되어야 할 것들 (공통)
- Map의 형태 (x좌표, y좌표), Graph의 형태 (Vertex, Edge), 두 가지 형태가 있다.
- 각 유형에 맞춰 직관적으로 이해할 수 있도록 변수이름을 설정한다.
- 각 정점 또는 포인트 (x, y) 가 방문되었는지 여부를 확인하는 1차원 배열이 필요하다. (visited)
- Map의 경우, 해당 포인트가 존재 (ex. 집이 있다) 하거나 Graph의 경우, 각 정점끼리의 간선이 존재 (ex. 연결되어 있다, 길이 있다) 라면 해당 배열 인덱스의 값을 1로 바꿔준다.

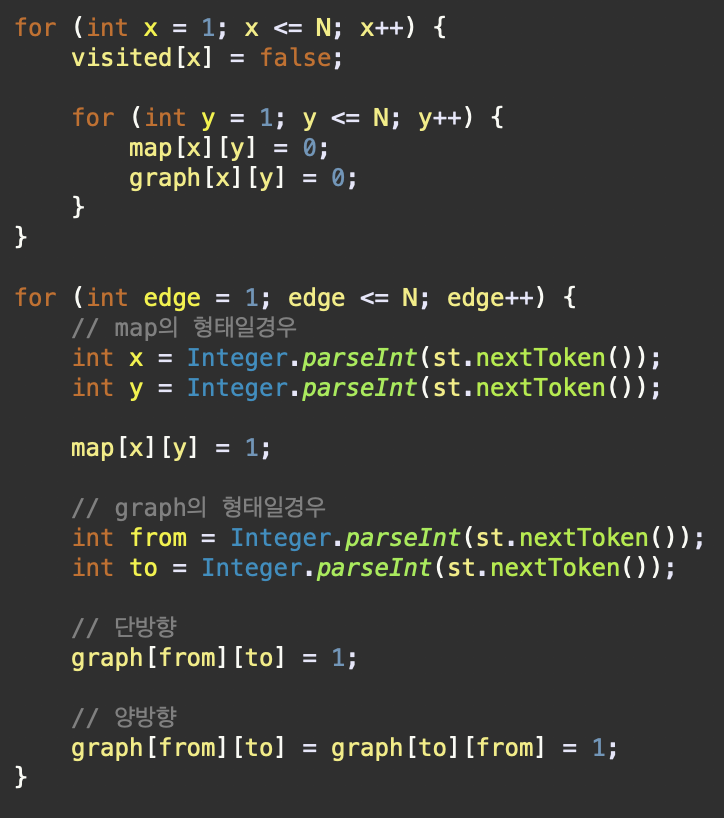
DFS의 핵심 부분
- 1. 재귀 (Recursion)
- 재귀의 경우, from 정점과 to 정점이 연결되어 있고 (graph[from][to] = 1), 아직 방문하지 않았다면 (visited[to] == false),
- DFS를 다시 호출하되 from을 to로 바꿔서 호출한다.
- ex) from = 1, to = 4 -> from = 4, to = 5 식으로 진행된다. (연결되어 있다면)

- 2. 스택 (Stack)
- 스택의 경우, Top에 있는 정점과 연결되어 있고 아직 방문하지 않은 정점을 찾는다.
- 조건에 맞는 정점을 찾았다면, 해당 정점을 스택에 Push하고 빠져나온다.
- 조건에 맞는 정점을 찾지 못했다면, Top에 있는 정점을 Pop 한다.
- 핵심은 if문 내에서 break를 통해 정점과 연결된 정점을 찾을 경우, for문을 빠져나옴으로써 DFS 탐색이 진행된다.

BFS의 핵심 부분
- 1. 큐 (Queue)
- 먼저 큐의 맨 앞인 front 정점 (nfrom) 과 연결된 모든 정점들 (to) 을 찾아 큐에 집어 넣는다 (for 문을 통해). 연결되지 않았다면 큐에 들어가지 않을 것이다.
- 위의 1번 과정을 큐가 비어 있지 않은 동안 계속 반복한다. 큐가 비었다면 조건에 만족 (정점이 연결되어 있다) 하는 정점이 없는 것이다.
- 따라서 BFS의 경우는 넓이를 우선적으로 탐색하기 때문에 최단 경로에 이용한다.

Map 유형
- 위 코드들은 모두 Graph 유형인 경우이지만, Map 형태의 경우는 큰 차이점은 없지만, 약간의 다른 점은 그래프는 다음 정점 (정점 숫자) 을 저장하지만, 맵은 다음 포인트 (x, y 좌표) 를 각 방법에 따라 전달한다.
- 보통 동서남북으로만 한칸씩 움직일 수 있다는 조건이 나온다. 따라서 각 방향에 대해 좌표를 이동하는 배열을 만들어준다.
- BFS를 예시로 설명하도록 하겠다.
- 먼저 x, y좌표를 저장할 포인트 클래스를 만들어준다.
- 이제 큐에 정점 숫자를 삽입하는 것이 아닌 포인트 객체를 삽입한다.
- 큐의 Front 좌표에서 동서남북 방향을 확인하며 조건에 맞는 좌표 (ex. 동서남북 방향이 맵 안쪽에 위치한다, 집이 있다) 가 있다면 큐에 삽입한다.
- 2번과 3번을 계속 반복하면 된다.


- dx, dy 배열이 동서남북 방향으로 한 칸 이동하는 것이다.
- nx, ny는 동서남북 방향으로 이동한 nextx, nexty 좌표이다.
- visited 배열의 경우 그래프에서는 정점을 방문했는지 여부를 확인하기 위해 1차원으로 선언하였지만, 맵의 경우 해당 좌표가 방문되었는지를 확인하기 위해 2차원 배열 (x, y) 로 사용한다.
Reference
반응형
'Algorithm > Technique' 카테고리의 다른 글
| 최소 스패닝 트리 (MST, Minimum Spanning Tree) : 크루스칼 (Kruskal) (0) | 2019.12.10 |
|---|---|
| 소수 (Prime Number) & 에라토스테네스의 체 (Eratosthenes's Sieve) (0) | 2019.12.05 |
| KMP (Knuth–Morris–Pratt) (0) | 2019.11.26 |
| 벨만-포드 (Bellman-Ford) (0) | 2019.11.17 |
| 플로이드 와샬 (Floyd Warshall) (0) | 2019.10.31 |
댓글
