티스토리 뷰
반응형
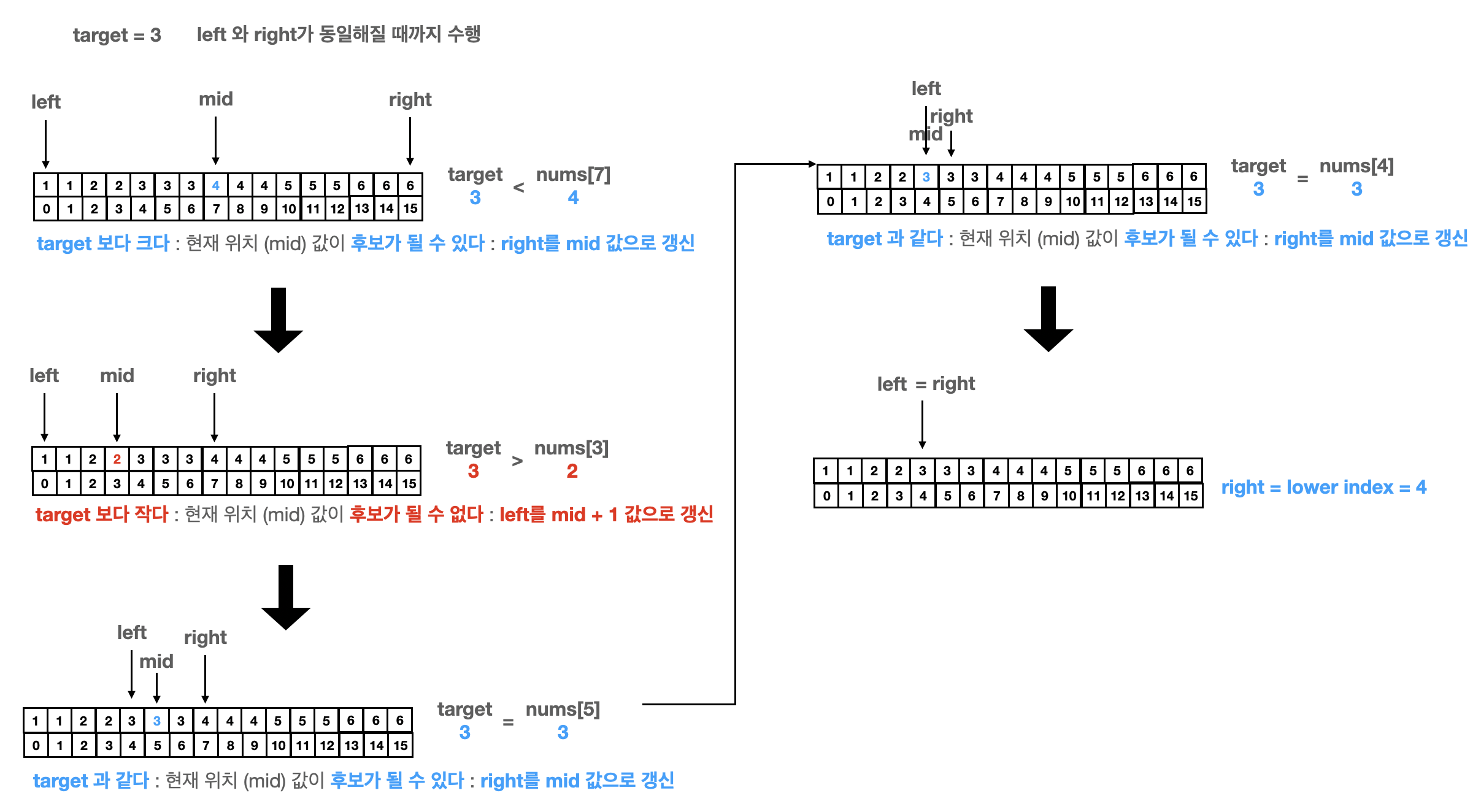
Lower Bound
찾고자 하는 target 이상의 값이 인덱스 0부터 시작했을 때 등장하는 최초의 위치
과정
코드
public static int lowerBound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
// 찾으려고 하는 target 값이 현재 nums[mid] 값보다 작거나 같다면
// nums[mid]는 후보가 될 수 있는 값이다.
if (target <= nums[mid])
right = mid;
else
left = mid + 1;
}
return right;
}
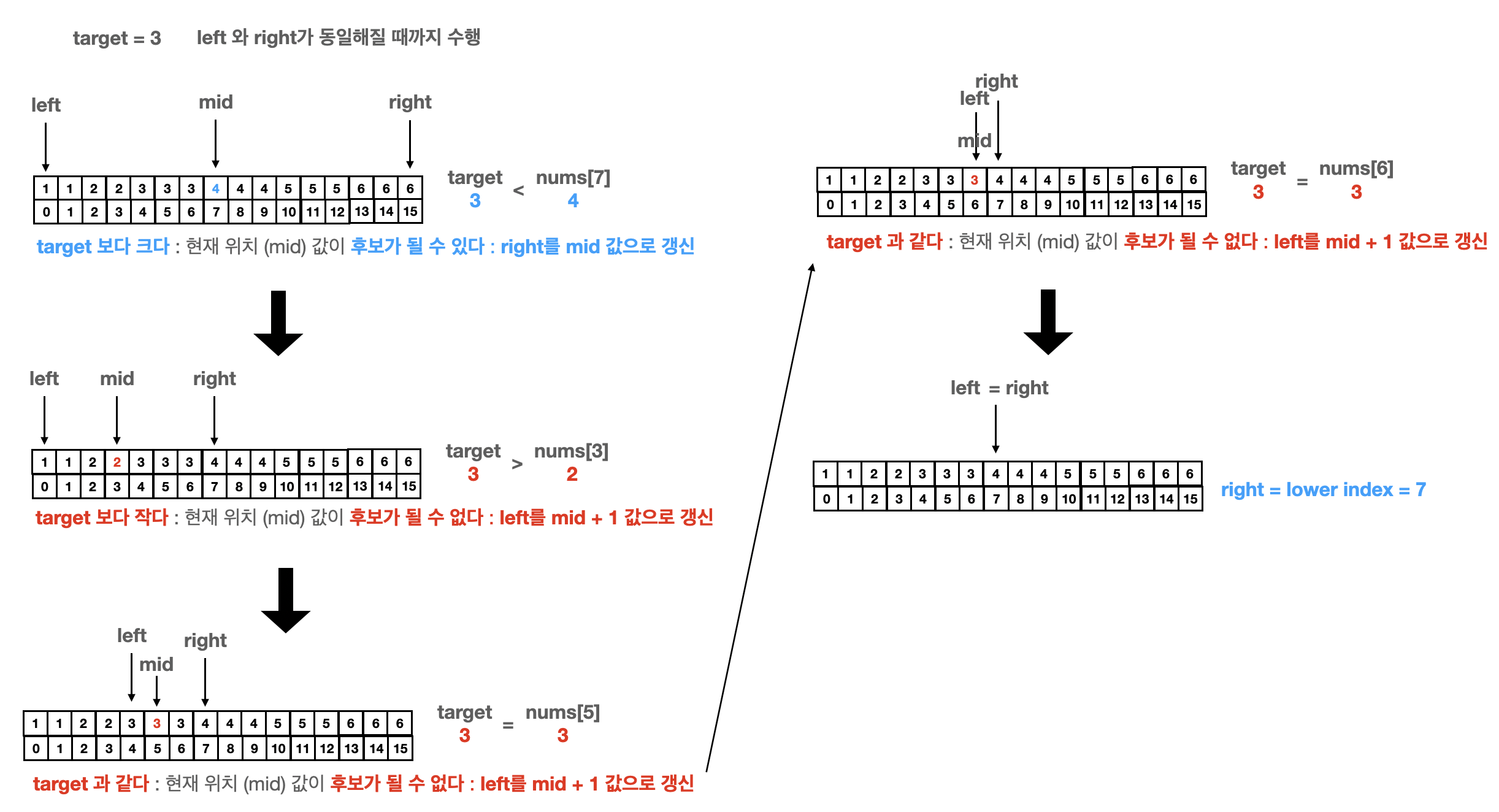
Upper Bound
찾고자 하는 target을 초과하는 (target을 포함하지 않음) 값이 등장하는 최초의 위치
과정
코드
public int upperBound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
// Lower Bound와 다른점은 '=' 등호가 빠졌다는 것.
if (target < nums[mid])
right = mid;
else
left = mid + 1;
}
return right;
}
결과

계산 복잡도
Time Complexity : Binary Search를 이용하여 탐색하므로 O(logN)
Space Complexity : O(1)
반응형
'Algorithm > Technique' 카테고리의 다른 글
| 네트워크 유량 (Network Flow) (0) | 2020.03.24 |
|---|---|
| 최소 스패닝 트리 (MST, Minimum Spanning Tree) : 프림 (Prim) (0) | 2019.12.10 |
| 최소 스패닝 트리 (MST, Minimum Spanning Tree) : 크루스칼 (Kruskal) (0) | 2019.12.10 |
| 소수 (Prime Number) & 에라토스테네스의 체 (Eratosthenes's Sieve) (0) | 2019.12.05 |
| KMP (Knuth–Morris–Pratt) (0) | 2019.11.26 |
댓글
