티스토리 뷰
반응형
A / B Testing 의 단점을 보완
- A / B Testing : A / B Testing URL
- A / B Testing이 단점을 간단히 얘기하면 다음과 같다.
- 테스트를 많이 하면 단기적으로 손해가 발생할 수 있다.
- A / B Testing의 결과는 시간의 흐름 (계절 / 취향 변화) 에 따라 바뀔 수 있다.
MAB (Multi-Armed Bandits) ?
- A / B Testing의 문제를 해결하기 위해 실험을 길게 하거나, 일정한 주기로 동일한 실험을 반복하는 방식으로 보완할 수는 있지만 비효율적이다.
- 아래 그림은 카카오의 추천 AI 플랫폼인 '토로스'의 내부 로직이다. MAB가 어느 시점에 쓰이는지 직관적으로 알 수 있다.

어원 및 정의
- A / B 테스트가 가진 문제점을 해결한다고 알려진 MAB의 어원을 먼저 살펴보자.
- MAB (Multi-Armed Bandit) 라는 말은 슬롯머신을 One-Armed Bandit (외팔 도둑, 슬롯머신에 있는 손잡이를 지칭) 이라고 부르는 데서 기인한 이름이라고 한다.
- 정확한 승률을 알지 못하는 여러 대의 슬롯머신을 가지고 도박을 할 때, 가장 많은 돈을 따고 싶지만 각 슬롯마다 보상 (Reward) 확률이 다르고 어떤 슬롯의 보상이 가장 큰 지 모른다.
- 이러한 상황에서 '어떤 순서로 어떤 슬롯을 얼마나 당겨야 가장 많은 돈 (보상) 을 딸 수 있을 것인가' 하는 문제를 빗대어서, 잡아당길 수 있는 여러 개의 손잡이를 가진 슬롯머신을 MAB 라고 부르게 된 것이다.
Exploration (탐색) & Exploitation (수확)
- 각 슬롯머신의 승률을 확인하기 위한 과정을 탐색 (Exploration) 이라고 할 수 있다.
- 가장 높은 승률을 가진 슬롯머신을 파악하기 위해서 슬롯 머신을 플레이하는 과정이다.
- 어떤 슬롯머신의 승률이 높은지 알아내야 하기 때문에, 승률이 낮은 슬롯머신으로 플레이해보는 것을 피할 수는 없다.
- 반면, 수확 (Exploitation) 은 가장 높은 승률을 가진 것으로 예상되는 슬롯머신을 선택해서 본격적으로 돈을 따는 과정이라 볼 수 있다.
- 과정을 치르는 동안 두 가지 모두 비용이 발생하고, 게임을 할 수 있는 횟수는 줄어들기 때문에 슬롯머신 선택 (탐색, Exploration) 과 손잡이를 내릴 횟수 (수확, Exploitation) 를 어떻게 조정하느냐에 따라 최대로 돈을 딸 수 있는 확률이 달라질 수 있다.
- 정보를 얻어 가장 좋은 승률을 가진 슬롯머신을 선택해야 하기 때문에 이 두 과정이 반드시 필요하며, 한 가지 과정을 완전히 배제해서는 원하는 결과를 얻을 수 없다 (Trade-off).
- 이 때문에 Bandit 문제를 '탐색 / 수확 딜레마 (Exploration / Exploitation Dillema)' 라고도 부른다.
MAB Algorithm
- 탐색과 수확의 비율을 어떻게 조정하냐에 따라 여러 전략이 나올 수 있을 것이다.
- 전통적인 A / B Testing을 MAB 문제 관점에서 서술하면 "짧게 Exploration & 평생 Exploitation" 전략이라고 볼 수 있다.
- 하지만, 이는 세상이 변하지 않는다는 가정이 있을 때 적합한 전략이지만, 비즈니스 환경에서는 이러한 가정을 하기 어렵다.
Greedy Algorithm
- 모든 슬롯머신을 한 번씩 플레이 한 후, 돈을 가장 많이 딴 슬롯머신에 모두 투자한다.
- 하지만, 이러한 전략의 문제는 한 번씩만 테스트를 진행한 것이기 때문에 충분한 탐색 (Exploration) 이 이루어지지 않았다는 것이다.
The ε (epsilon) - Greedy Algorithm
- Bandit Problem을 해결할 수 있는 간단한 알고리즘이다.
- 이 알고리즘은 1 − ε 의 확률로 지금까지 관측한 가장 돈을 많이 딸 수 있는 슬롯머신을 선택하고 (Exploitation), ε의 확률로 나머지 슬롯머신 중에서 무작위로 하나의 슬롯머신을 탐색하는 (Exploration) 알고리즘이다.
- 이 알고리즘은 뒤에서 설명할 다른 알고리즘들보다 이론적으로, 그리고 실험적으로 우수하지는 못하지만, 매우 직관적이다.
- 이 알고리즘의 파라미터 ε 자체가 Exploration & Exploitation Trade-off를 조절하는 Term이 된다.
- ε의 값이 크면 그만큼 탐색 (Exploration) 을 많이 하게 되고, 반대의 경우도 마찬가지로 생각할 수 있다.

단점
- 어느정도 시간이 지나 최적의 슬롯머신을 찾았더라도, 계속해서 ε만큼의 탐색 (Exploration) 을 해야하기 때문에 최적 값과 멀어지는 결과를 초래한다.
- ε의 확률로 Sub-optimal 한 나머지 슬롯머신들을 무작위로 뽑기 때문에, 전체 슬롯머신 중에서 탐색하지 못하거나, 혹은 탐색을 덜하여 정보를 많이 얻지 못한 슬롯머신이 생길 가능성이 크다.
The Softmax Algorithm
- 지금까지 알려진 성과를 기반으로 성과가 좋은 쪽에 사용자를 좀 더 몰아주는 알고리즘(Softmax)
- ε - Greedy 알고리즘을 예시로 봐보자.
- 시나리오 A와 B가 있다고 해보자.
- 시나리오 A에서는 두 개의 슬롯머신을 가지고 있으며, 하나는 10%의 보상을 주며, 나머지 하나는 13%의 보상을 준다.
- 시나리오 B 에서도 마찬가지로 두 개의 슬롯머신이 있으며, 하나는 10%, 다른 하나는 99%의 보상을 준다.
- 이 두 시나리오에서, ε - Greedy 알고리즘은 시나리오 A의 열등한 슬롯머신이 시나리오 B의 열등한 슬롯머신보다 훨씬 더 나쁨에도 불구하고 정확히 동일한 확률 (ε / 2) 로 탐색한다.
- 위 과정이 문제가 되는 이유는 아래와 같다.
- 두 슬롯머신의 보상 비율 차이가 작을 경우, 두 옵션 중 실제로 어떤 것이 더 좋은지 정확히 결정하기 위해 10% 이상의 시간 (10% of Time) 으로 더 많이 탐색해야 할 것이다.
- 반대로 보상 비율 차이가 클 경우, 두 옵션 중 더 좋은 것을 정확히 추정하기 위해 10% 미만으로 탐색해야 한다.
- 그러한 이유로, 애매한 더 낮은 옵션을 탐색함으로써 많은 보상을 잃게 될 것이다.
- 즉, ε - Greedy 알고리즘의 무작위 탐색으로 인한 시간낭비를 줄이기 위해 구조적인 탐색이 필요하다는 것이다.
예시 설명
- A, B 두 개의 슬롯머신이 있다고 해보자.
- 과거 경험을 바탕으로, 이 두 슬롯머신이 각각 rA, rB 라는 서로 다른 성공률을 가지고 있는 것을 알고 있다.
- 이러한 상황에서 Softmax 알고리즘을 가장 Naive하게 구현할 경우, 슬롯머신 A는 rA / (rA + rB ), 슬롯머신 B는 rB / (rA + rB ) 확률로 선택될 수 있다.
- 하지만, 사람들이 실제로 사용하는 알고리즘으로 재구성하려면, 두 가지를 변경해야 한다.
첫 번째 변경
- rA 와 rB 의 추정치를 거듭제곱 (Exponentiating) 하여 다른 척도로 보상 비율을 계산하며, 다음과 같이 확률을 변경한다.

- 더 중요한 것은 이 거듭제곱 트릭은 완전한 Softmax 알고리즘에 매우 근접하게 해준다.
- 여기서 표준 Softmax 알고리즘이 가지고 있는 파라미터 하나를 더 추가하면 된다.
두 번째 변경
- 이 새로운 타입의 스케일링 인자는 일반적으로 고온의 시스템이 저온에서 더 많은 구조를 취하면서 무작위로 동작하는 경향이 있는 물리학과 유사하게 온도 파라미터라고 불린다.
- 우리는 이 새로운 온도 파라미터를 tau 라고 부를 것이다.
- 시간 T에서 아래와 같이 계산된 확률로 두 개의 슬롯 머신 중 하나를 선택한다.

- 이후의 과정은 ε - Greedy 알고리즘과 동일하다.
tau는 무슨 역할 ?
- tau는 우리가 슬롯머신을 선택하는 극단적인 방법으로 정의되는 연속체 (Continuum) 를 따라 Softmax 알고리즘의 동작을 이동하게 하는 것으로 생각하는 것이 가장 쉽다.
- 한 극단 (Extreme) 에서 tau = 0.0을 설정하면, 추정치가 가장 높은 슬롯머신의 완전히 결정론적인 선택을 줄 것이다.
- 다른 극단인 tau = INF 에서는 ε - Greedy 알고리즘과 같이 무작위 탐색을 할 것이다.
- 성과가 좋은 쪽에 사용자를 얼마나 더 몰아줄 것인지 ("온도") 를 조절할 수 있게 하는 방식 (Softmax + Temperature)
Annealing ?
- 시간이 흐르면서 알고리즘이 탐색을 적게 하도록 하는 것을 말한다.
- Softmax 알고리즘에서 온도를 천천히 낮춘다는 의미에서 어닐링 (Annealing) 이라 부른다.
- 시간이 지남에 따라 점진적으로 "온도"를 낮춰서 탐험 비율을 낮추는 방식 (Softmax + Temperature + Annealing)
UCB – The Upper Confidence Bound Algorithm
- 위 알고리즘들은 탐색했던 슬롯 머신으로부터 얼마나 많은 보상 (Reward) 을 받았는지에만 초점을 맞추며, 그들이 처음에 경험한 보상이 얼마 없던 슬롯머신들의 정보를 저장하지 않는다.
- UCB는 지금까지 알려진 보상뿐만 아니라, 그 보상이 얼마나 많은 탐색을 통해 알려진 결과인지 (즉, 얼마나 확실한지 [Uncertainty Weight]) 도 함께 따져서, 덜 확실한 쪽에 더 많은 탐색을 하는 방식이다.
장점
- 랜덤 탐색을 사용 하지 않고, 최적이 될 수 있을 만한 슬롯머신을 선택할 가능성을 수치로 계산한 뒤, 이 수치를 바탕으로 선택을 결정하기 때문에 어떻게 행동하는지 알 수 있다.
- 또한, 설정해야할 자유 (Free) 파라미터가 없다.
- 이는 세상이 어떻게 행동할지에 대한 명확한 감각을 갖지 않고도 UCB를 사용할 수 있다는 것을 의미한다.

- 빨간 네모 점선 수식이 의미하는 것은 선택한 슬롯머신이 최적의 슬롯머신이 될 가능성이다.
- \(t\) 는 모든 슬롯머신을 선택한 횟수의 합 (시점)
- \(Q_{t}(a)\) 는 \(t\) 시점까지 슬롯머신 \(a\) 의 누적 보상 (Reward)
- \(c\) 는 탐색의 정도를 결정하는 하이퍼 파라미터 (\(c\)가 크면 탐색을 많이 하며, 작다면 수확을 많이 수행)
- \(N_{t} (a)\) 는 \(t\) 시점 전까지 해당 슬롯머신을 선택했던 횟수
단점
- 매 라운드마다 수치 값을 갱신해줘야 한다.
- UCB를 계산하기 위해서는 Empirical Mean이 필수적이기 때문에 반드시 처음에는 모든 슬롯머신들을 한 번 이상 탐색 (Exploration ) 해야한다는 문제점이 있다.

Thomson Sampling
- Thompson sampling, 혹은 Probability Matching 알고리즘은 Google Analytics에서도 사용하고 있는 알고리즘으로 최근 이론적인 증명과 실험적인 결과에서 모두 두각을 보이고 있는 알고리즘이다.
- 값을 직접 추정하여 예측한 그대로 행동하는 결정론적인 (Deterministic) UCB 계열 알고리즘과 달리 기댓값의 사후 분포를 계산한 뒤 샘플링한 값을 기준으로 슬롯머신을 선택한다.
- 이 선택한 슬롯머신을 통해 얻은 보상을 바탕으로 베이지안 정리를 이용해서 분포를 갱신한다.
기본 아이디어
- 먼저 이 알고리즘은 베타 분포 (Beta Distribution) 를 사용한다.
베타 분포 (Beta Distribution) ?
- Beta 분포는 두 개의 양수 변수로 표현할 수 있는 확률 분포이며, α와 β 파라미터로 분포의 모양을 조절한다.


- 왜냐하면 광고를 클릭하는 것은 베르누이 (Bernoulli) 과정에 속하기 때문이다 (클릭의 유무는 1, 0으로 표현 가능하다).

예시 : 웹에 노출되는 배너
- 그림 출처 및 참고 : https://brunch.co.kr/@chris-song/66
- 이 예시에서 필요한 두 가지 숫자는 다음과 같다.
- 배너를 보고 클릭한 횟수
- 배너를 보고 클릭하지 않은 횟수

- 위 그래프를 통해서 다음과 같은 CTR이 나오게 될 것이다.
- 배너1 : 1번 성공 / 2번 시도 = 50%
- 배너2 : 0번 성공 / 2번 시도 = 0%
- 배너3 : 1번 성공 / 1번 시도 = 100%
톰슨 샘플링은 어떻게 동작 ?
- 확률밀도함수가 수렴하기 전까지는 샘플링이 수행되고 나면, 다른 배너들이 선택될 가능성이 있다.
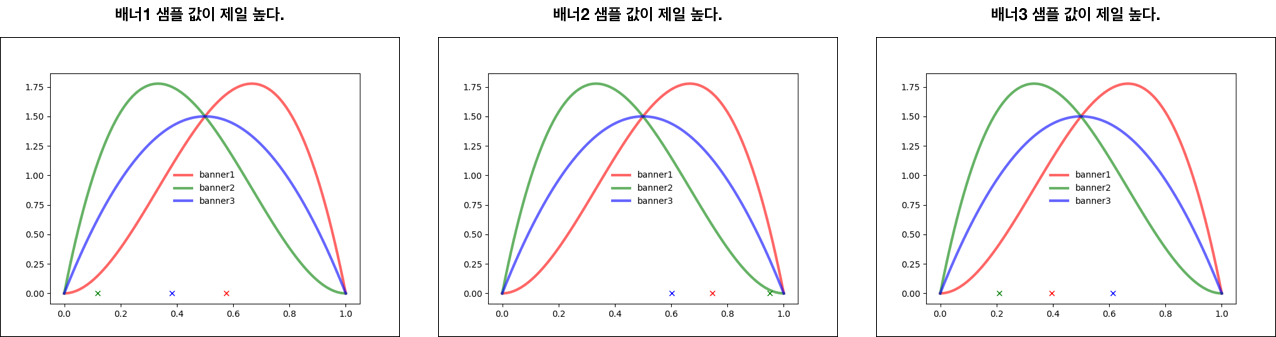
- 하지만, 여러번의 수행을 거쳐 어느정도 확률밀도함수가 수렴에 가까워지게 되면 샘플링 값을 여러차례 구해보아도 확률분포가 우세한 배너 그래프에서 선택이 되는 것을 볼 수 있다.
- 아래 두 그래프의 샘플링 값들은 미세하게 차이가 있지만 결국 배너3 그래프에서 선택된다.
- 수 많은 실험을 거쳐 아래와 같이 어떤 배너가 가장 반응이 좋은지 분포에서 명확하게 표현이 된다.
- 결국, 베이지안 추론을 통해 배너3이 가장 우수하다는 것을 알 수 있게 된다.

알고리즘 코드
- 확률분포에서 샘플링한 후 Argmax로 배너를 선택하고 결과를 관찰한 뒤에 그 결과를 확률 분포에 반영한다.

- 아래 코드를 보면 베타 분포에서 각 광고의 S (클릭 횟수), F (클릭하지 않은 횟수) 를 바탕으로 확률밀도함수 (PMF) 를 그린다 (Draw).
- 이 확률밀도함수에서 값들을 샘플링한 뒤, 뽑힌 값들 중 가장 큰 값의 광고를 선택한다 (Argmax).
- 이후에 CTR이 어떻게 바뀌었는지 탐색하고 클릭 성공 (S) 과 클릭 실패 (F) 를 기록하여 다시 톰슨샘플링을 반복한다.

- 아래 그림은 톰슨 샘플링의 논문에 있는 그림으로, UCB보다 톰슨 샘플링이 좋은 성능을 보인다는 것을 나타낸다.
- Regret은 최선의 선택에 비해 잘못된 선택을 함으로써 얼마나 손해를 입었는 지를 수치화한 것이다.

장점
- 확률적 알고리즘이다 (확률적으로 움직인다).
- 한 번에 하나의 슬롯머신만 플레이하는 싱글플레이 문제에서, N개의 슬롯머신을 플레이할 수 있는 멀티플레이 문제로의 확장이 용이하다는 것이다.
- 액션을 최대화하는 문제를 만족하는 M개의 액션을 순서대로 고르는 방법 (MP-TS, Multiplay Thompson Sampling)
- N - 1 개의 슬롯머신은 경험적인 결과가 가장 좋은 슬롯머신을 고르고, 마지막 N번째 슬롯머신만 Thompson Sampling으로 푸는 방법 (IMP-TS, Improved MP-TS)
- 실제로는 두 번째 방법이 Asymptotic Bound를 유지하면서 성능이 조금 더 좋다고 한다.
- 나중에 들어오는 피드백 데이터도 수용할 수 있다 (회원가입 / 결제 데이터 ...)
문제점
- 시간의 흐름에 따라 α + β 값이 계속해서 증가하므로 Algorithm 1의 모델 파라미터 에 대한 추정을 하기 점점 어려워진다.
- 이러한 문제를 해결하는 간단한 방법 중 하나는 Discounted Thompson Sampling을 사용하는 것이다.
카카오 루빅스의 맞춤형 MAB 알고리즘
변화하는 클릭율
- 카카오에서는 다음과 같이 MAB를 뉴스 기사 문제에 매칭했다 :
- 슬롯 머신 -> 개별 뉴스
- 슬롯 머신의 승률 -> 뉴스가 클릭 될 확률 (CTR, Click Through Rate)
- 기대보상 -> 총 뉴스 클릭수
- 일반적으로 MAB 알고리즘에서 각 슬롯 머신의 승률은 고정값이지만, 뉴스의 CTR은 시간에 따라 변하며 경과된 시간이 길어질수록 뉴스가 덜 소비되는 경향이 있다.

- 이처럼 동일한 뉴스라 하더라도 각 뉴스의 CTR은 시간의 경과에 따라 끊임없이 변하기에, 적절한 추천을 위해서 알고리즘이 뉴스의 CTR을 지속적으로 측정해야 한다.
- 이는 Softmax나 UCB 알고리즘 방식이 뉴스 서비스 추천에서는 효과적으로 작동하지 않을 수 있음을 의미한다.
- 또한, 새로운 뉴스 기사 (슬롯 머신) 이 끊임없이 추가되고, 동시에 기존 뉴스 기사가 지속적으로 사라지는 특징 역시 뉴스 서비스가 전통적인 MAB 구조와 다른 점이다.
이러한 환경에서 담금질 전략은 끊임없이 초기화되기 때문에 효율성이 떨어진다.
- 담금질 ? - 전체 탐색 횟수에 반비례해서 탐색 비율을 줄이는 전략.
- 즉, 탐색이 충분히 이뤄졌다면, 추가적인 탐색 (Exploration) 횟수를 줄이고 수확 (Exploitation) 의 비율을 늘림으로써 기대 보상을 증대하는 것이다.
- 그러나, 새로운 뉴스가 들어오면 전체 탐색횟수가 0으로 초기화 되며, 다시 충분한 수준의 탐색이 필요하게 된다.
루빅스는 어떻게 ?
- 매 분 단위로 각 뉴스의 CTR (슬롯 머신의 승률) 을 측정한다.
- 단, 1분이라는 단위 시간이 상대적으로 짧다보니, 표본의 부족으로 인해 CTR이 부정확하게 측정될 수도 있다.
- ex) 10번의 노출 중 1번 클릭되어 도출된 10% CTR과 1만 번 노출하여 1000번 클릭된 결과로 계산된 10% CTR은 동일하게 취급될 수 없다.
- 이와 같은 통계적 부정확성을 극복하고 정확한 실시간 CTR을 측정하기 위해서, 루빅스에는 이동 평균 (Moving Average) 알고리즘이 사용됐다.
이동 평균 (Moving Average) 알고리즘 ?
- 분 단위 측정을 하면서 과거 데이터까지 모두 사용하는 동시에 최신 데이터일수록 더 많은 가중치를 줘, 이용자의 최신 뉴스 패턴을 반영함으로써 CTR 측정의 신뢰도를 높일 수 있다.

뉴스 위치에 따른 클릭율 변화
- 전통적인 MAB 알고리즘에서는 수확 (Exploitation) 을 위해 하나의 슬롯 머신만 선택하지만, 뉴스 추천에서는 여러 개의 뉴스를 동시에 추천한다.
- 동시에 여러 개의 뉴스가 추천되다 보니, 뉴스는 화면 내 각기 다른 위치에 배치되고, 이 위치에 따라 CTR이 변한다.
- 이를 위치 편향 (Position Bias) 라고 한다.
- 루빅스는 위치 편향 현상을 해소하기 위해서 '이중의 탐색' 을 실행한다.
이중의 탐색 ?
- 이 탐색을 이용해서 CTR을 계산하면 평균 위치에서의 기사 CTR이 계산된다.
- N 개의 위치가 있다면 모든 위치에서 '\(\frac{1}{N} \times 총 탐색 수\)' 만큼 동일하게 검증이 이루어지고 이들의 평균으로 CTR이 계산되는 것이다.
- 이 결과로 나온 '평균 위치에서의 기사 CTR' 은 기사 자체가 얼마나 선호되는가를 의미하게 되며, 이를 기사의 '선호도'로 정의한다.
이용자 집단별 최적화
- 루빅스의 맞춤형 MAB는 각 이용자 집단 (성별이나 연령대) 의 뉴스 소비 패턴에 근거하여 해당 집단에 속한 개인에게 뉴스를 추천한다.
- ex) 20대 여성 - 뷰티 및 취업, 30대 여성 - 육아, 40대 여성 - 교육 ...
- 스포츠 영역에서는 이용자들의 뉴스 소비 패턴에 기반을 두어 이용자를 따로 분류하는 '클러스터링 (Clustering)' 방식을 적용했다.
Reference
- https://brunch.co.kr/@kakao-it/72
- http://www.ecogwiki.com/Bandit_Algorithms_for_Website_Optimization
- https://wwiiiii.tistory.com/entry/MultiArmed-Bandit-Problem
- http://doc.mindscale.kr/km/data_mining/11.html
- https://tkdguq05.github.io/2019/07/18/Bandit/
- http://sanghyukchun.github.io/96/
- https://brunch.co.kr/@chris-song/62
- http://hub.zum.com/kimws/2586
- http://www.ecogwiki.com/A-B_Testing의_단점과_개선안
- https://vwo.com/blog/multi-armed-bandit-algorithm/
- http://papers.nips.cc/paper/4321-an-empirical-evaluation-of-thompson-sampling.pdf
구현
반응형
'Recommendation' 카테고리의 다른 글
| A / B Testing (0) | 2020.01.14 |
|---|
댓글
